题目内容
已知函数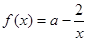 。
。
(1)讨论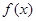 的奇偶性;
的奇偶性;
(2)判断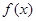 在
在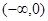 上的单调性并用定义证明。
上的单调性并用定义证明。
【答案】
(1)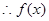 不具备奇偶性
不具备奇偶性
(2)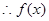 在
在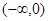 上单调递增
上单调递增
【解析】
试题分析:解:(1)函数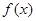 的定义域为
的定义域为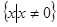 关于原点对称。
1分
关于原点对称。
1分
(1)方法1: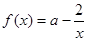 ,
,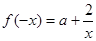 2分
2分
若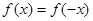 ,则
,则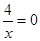 ,无解,
,无解,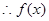 不是偶函数
4分
不是偶函数
4分
若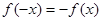 ,则
,则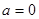 ,显然
,显然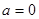 时,
时,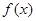 为奇函数
为奇函数
综上,当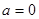 时,
时,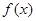 为奇函数;当
为奇函数;当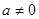 时,
时,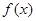 不具备奇偶性 6分
不具备奇偶性 6分
方法2:函数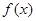 的定义域为
的定义域为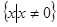 关于原点对称。
1分
关于原点对称。
1分
当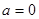 时,
时,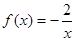 ,
,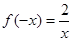 ,
,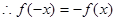 ,
,
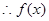 为奇函数:
4分
为奇函数:
4分
当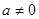 时,
时,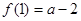 ,
,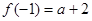 ,显然
,显然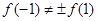
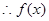 不具备奇偶性。
6分
不具备奇偶性。
6分
(2)函数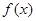 在
在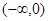 上单调递增; 7分
上单调递增; 7分
证明:任取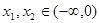 且
且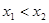 ,则
,则
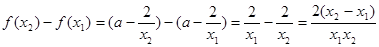 9分
9分
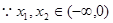 且
且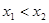 ,
,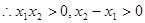 ,
,
从而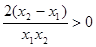 ,故
,故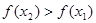 , 11分
, 11分
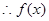 在
在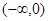 上单调递增。
12分
上单调递增。
12分
考点:函数的奇偶性和单调性
点评:解决的关键是对于函数奇偶性和单调性概念的准确判定和运用,属于基础题。

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
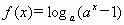 ,(
,(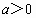 ,
,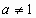 ),
),
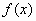 的定义域;
的定义域;
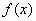 的单调性.
的单调性.