题目内容
已知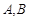 是椭圆
是椭圆 和双曲线
和双曲线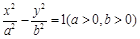 的公共顶
的公共顶
点。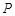 是双曲线上的动点,
是双曲线上的动点,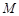 是椭圆上的动点(
是椭圆上的动点(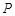 、
、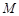 都异于
都异于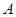 、
、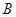 ),且满足
),且满足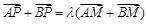 ,其中
,其中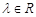 ,设直线
,设直线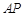 、
、 、
、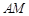 、
、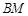 的斜率 分别记为
的斜率 分别记为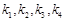 ,
, 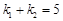 ,则
,则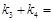
-5
解析试题分析:∵A,B是椭圆 和双曲线
和双曲线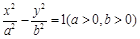 的公共顶点,
的公共顶点,
∴(不妨设)A(-a,0),B(a,0).
设P(x1,y1),M(x2,y2),∵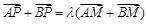 ,其中λ∈R,
,其中λ∈R,
∴(x1+a,y1)+(x1-a,y1)=λ[(x2+a,y2)+(x2-a,y2)],化为x1y2=x2y1.
∵P、M都异于A、B,∴y1≠0,y2≠0.∴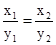 .
.
由k1+k2=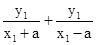 =5,化为
=5,化为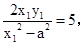 (*)
(*)
又∵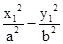 =1,∴
=1,∴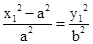 ,代入(*)化为
,代入(*)化为 .
.
k3+k4=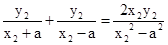 ,又
,又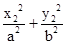 =1,
=1,
∴ ,
,
∴k3+k4=-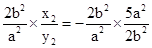 =-5.
=-5.
故答案为-5.
考点:椭圆、双曲线的标准方程及几何性质,平面向量的坐标运算,直线的斜率及其坐标运算。
点评:难题,熟练掌握点在曲线上的意义、双曲线和椭圆的方程、向量的坐标运算、斜率的计算公式是解题的关键,同时本题计算能力要求较高。

练习册系列答案
相关题目
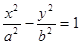 的渐近线方程是
的渐近线方程是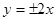 ,那么此双曲线的离心率为 .
,那么此双曲线的离心率为 .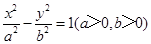 的左顶点与抛物线
的左顶点与抛物线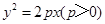 的焦点的距离为
的焦点的距离为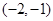 ,则双曲线的焦距为 .
,则双曲线的焦距为 .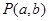 与点
与点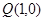 在直线
在直线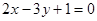 的两侧,则下列说法:
的两侧,则下列说法: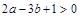 ;
; 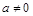 时,
时,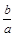 有最小值,无最大值;
有最小值,无最大值;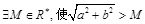 恒成立
恒成立 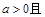
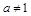 ,
,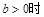 , 则
, 则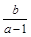 的取值范围为(-
的取值范围为(-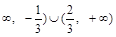
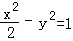 ,曲线C2:|y|=|x|+1,P是平面内一点,若存在过点P的直线与C1,C2都有公共点,则称P为“C1﹣C2型点“
,曲线C2:|y|=|x|+1,P是平面内一点,若存在过点P的直线与C1,C2都有公共点,则称P为“C1﹣C2型点“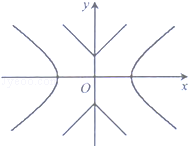
 内的点都不是“C1﹣C2型点”
内的点都不是“C1﹣C2型点”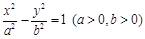 与抛物线
与抛物线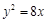 有一个公共的焦点,且双曲线上的点到坐标原点的最短距离为1,则该双曲线的标准方程是___________。
有一个公共的焦点,且双曲线上的点到坐标原点的最短距离为1,则该双曲线的标准方程是___________。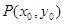 是抛物线
是抛物线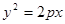 上一点,则该点到抛物线的焦点的距离是
上一点,则该点到抛物线的焦点的距离是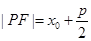 ;
; 、
、 为双曲线
为双曲线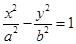 的两个焦点,
的两个焦点,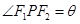 ,则
,则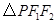 的面积为
的面积为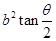 ;
;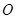 上有一动点
上有一动点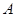 ,圆
,圆 ,
,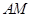 的垂直平分线与半径
的垂直平分线与半径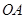 的交点为点
的交点为点 ,则
,则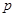 ,过抛物线焦点
,过抛物线焦点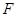 的直线交抛物线于A、B两点,则
的直线交抛物线于A、B两点,则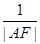 、
、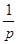 、
、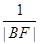 成等差数列.
成等差数列.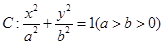 的左焦点为
的左焦点为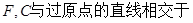
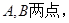
 .
.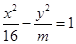 的离心率为
的离心率为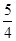 , 则m等于 .
, 则m等于 .