题目内容

（2013•德州一模）直线x+
3
y-2
3
=0与圆x2+y2=4交于A，B两点，则
OA
•
OB
=（　　）
分析：由点到直线的距离公式，结合圆的性质可得向量的夹角∠AOB=60°，模长都为圆的半径2，由数量积的定义可得．
解答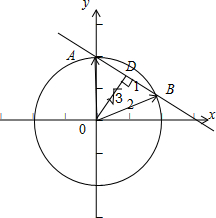：解：由题意可得直线x+
3
y-2
3
=0到圆心（0，0）
的距离d=
|-2
3
|
12+(
3
)2
=
3
，故BD=1，∠BOD=30°
故可得向量的夹角∠AOB=60°，
故
OA
•
OB
=2×2×cos60°=2
故选C
点评：本题考查平面向量数量积的运算，涉及直线与圆的位置关系，属中档题．
练习册系列答案
相关题目
（2013•德州一模）命题“?x∈R，x2-2x=0”的否定是（　　）
（2013•德州一模）在△ABC中，角A，B，C的对边分别为a，b，c，已知角A=
π
3
，sinB=3sinC．
（1）求tanC的值；
（2）若a=
7
，求△ABC的面积．
（2013•德州一模）若正项数列{an}满足1gan+1=1+1gan，且a2001+a2002+a2003+…a2010=2013，则a2011+a2012+a2013+…a2020的值为（　　）
（2013•德州一模）直线y=-
3
3
x+m与圆x2+y2=1在第一象限内有两个不同的交点，则m取值范围是（　　）
（2013•德州一模）设集合A={x|x2-5x-6＜0}，B={x|5≤x≤7}，则A∩B=（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网