题目内容
已知函数f（x）=sin2x-2cos2x（x∈R）．
（Ⅰ）求函数f（x）的最小正周期；
（Ⅱ）求函数f（x）的单调递增区间，并写出对称轴方程．
解：（1）f（x）=sin2x-2cos2=sin2x-cos2x-1，--------（2分）
则
，----------（4分）
所以，函数f（x）的最小正周期为π．------（6分）
（2）由
，得
．------（8分）
所以，函数f（x）的单调递增区间为：
．-------（9分）
从
，得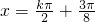
，--------（11分）
故对称轴方程为：
．--------（12分）
分析：（1）三角函数的恒等变换化简f（x）的解析式为
，由此求得函数的周期．
（2）由，求得x的范围，即可求得f（x）的单调递增区间．由，求得对称轴方程．
点评：本题主要考查三角函数的恒等变换及化简求值，三角函数的对称性、周期性和求法，属于中档题．
则
，----------（4分）所以，函数f（x）的最小正周期为π．------（6分）
（2）由
，得．------（8分）所以，函数f（x）的单调递增区间为：
．-------（9分）从
，得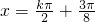，--------（11分）故对称轴方程为：
．--------（12分）分析：（1）三角函数的恒等变换化简f（x）的解析式为
，由此求得函数的周期．（2）由
，求得x的范围，即可求得f（x）的单调递增区间．由，求得对称轴方程．点评：本题主要考查三角函数的恒等变换及化简求值，三角函数的对称性、周期性和求法，属于中档题．
练习册系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
