题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,且acosC,bcosB,ccosA成等差数列.(Ⅰ)求角B的大小;
(Ⅱ)若a+c=4,求AC边上中线长的最小值.
【答案】分析:(Ⅰ)由已知,2bcosB=ccosA+acosC,利用正弦定理,将边b,c,a代换成sinB sinC sinA,再利用两角和正弦公式求B
(Ⅱ)设AC边上的中点为E,利用三边a,b,c用余弦等量将中线BE表示出来,再用基本不等式求最小值.
解答:解:(Ⅰ)由题意得:2bcosB=ccosA+acosC,
2sinBcosB=sinCcosA+sinAcosC,
2sinBcosB=sinB,
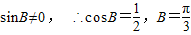 .
.
(Ⅱ)如图:设AC边上的中点为E,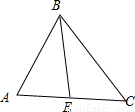
在△BAE中,由余弦定理得: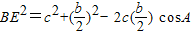 ,
,
又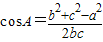 ,a2+c2-b2=ac代入上式,并整理得
,a2+c2-b2=ac代入上式,并整理得
BE2=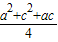
=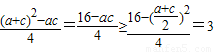 ,当a=c=2时取到”=”
,当a=c=2时取到”=”
所以AC边上中线长的最小值为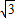 .
.
点评:本题考查正弦、余弦定理的应用,用基本不等式求最值.考查分析解决、计算能力.
(Ⅱ)设AC边上的中点为E,利用三边a,b,c用余弦等量将中线BE表示出来,再用基本不等式求最小值.
解答:解:(Ⅰ)由题意得:2bcosB=ccosA+acosC,
2sinBcosB=sinCcosA+sinAcosC,
2sinBcosB=sinB,
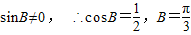 .
.(Ⅱ)如图:设AC边上的中点为E,

在△BAE中,由余弦定理得:
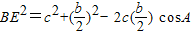 ,
,又
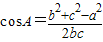 ,a2+c2-b2=ac代入上式,并整理得
,a2+c2-b2=ac代入上式,并整理得BE2=
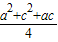
=
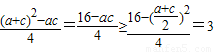 ,当a=c=2时取到”=”
,当a=c=2时取到”=”所以AC边上中线长的最小值为
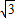 .
.点评:本题考查正弦、余弦定理的应用,用基本不等式求最值.考查分析解决、计算能力.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |