题目内容
设{an}是集合{2t+2s|0≤s<t且s,t∈Z}中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,…,将数列{an}各项按照上小下大,左小右大的原则写成如下的三角形数表.

(1)写出这个三角形数表的第四行与第五行各数;
(2)求a100.
解析:先将2n各数写出,再写出{an},并按由小到大排列即可写出三角形数表.
解:(1)第四行的数分别为17、18、20、24,第五行的数分别为33、34、36、40、48.
(2)设n为an的下标,
三角形数表第一行第一个元素下标为1.
第二行第一个元素下标为![]() +1=2.
+1=2.
第三行第一个元素下标为![]() +1=4.
+1=4.
……
第t行第一个元素下标为![]() +1.
+1.
第t行第s个元素下标为![]() +s.
+s.
该元素等于2t+2s-1.
据此判断a100所在的行为
![]() <100≤
<100≤![]() .
.
所以a100是三角形数表第14行的第9个元素,a100=214+29-1=16640.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
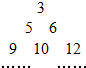 设an是集合2s+2t|0≤s<t,s,t∈Z中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,…,将数列an各项按照上小下大、左小右大的原则写成如下的三角形数表:
设an是集合2s+2t|0≤s<t,s,t∈Z中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,…,将数列an各项按照上小下大、左小右大的原则写成如下的三角形数表: 设{an}是集合{2t+2s|0≤s<t,且s,t∈z}中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,…将数列{an}各项按照上小下大,左小右大的原则写成如图的三角形数表:
设{an}是集合{2t+2s|0≤s<t,且s,t∈z}中所有的数从小到大排列成的数列,即a1=3,a2=5,a3=6,a4=9,a5=10,a6=12,…将数列{an}各项按照上小下大,左小右大的原则写成如图的三角形数表: