题目内容
17．（本题只限文科学生做）已知△ABC的两个顶点A（-10，2），B（6，4），垂心是H（5，2），求顶点C到直线AB的距离．
分析 求出直线AC，BC的方程，可得C的坐标，求出直线AB的方程，利用点到直线的距离公式求出顶点C到直线AB的距离．
解答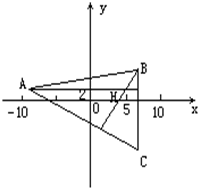 
解：∵${k_{BH}}=\frac{2-4}{5-6}=2$∴${k_{AC}}=-\frac{1}{2}$
∴直线AC的方程为$y-2=-\frac{1}{2}（x+10）$即x+2y+6=0 （1）
又∵kAH=0，
∴BC所直线与x轴垂直
故直线BC的方程为x=6 （2）
解（1）（2）得点C的坐标为C（6，-6）…（8分）
由已知直线AB的方程为：x-8y+26=0，
∴点C到直线AB的距离为：
d=$\frac{{|{6-8×（-6）+26}|}}{{\sqrt{1+64}}}$=$\frac{{16\sqrt{65}}}{13}$…（12分）
点评 本题考查直线方程，考查点到直线的距离公式，考查学生的计算能力，比较基础．
练习册系列答案
通城学典默写能手系列答案
相关题目
7．过两点（-1，0），（0，1）的直线方程为：（ ）
| A． | x-y+1=0 | B． | x-y-3=0 | C． | 2x-y=0 | D． | 2x-y-3=0 |
8．某同学参加4门学科的学业水平考试，假设该同学第一门学科取得优秀成绩的概率为$\frac{2}{3}$，第二门学科取得优秀成绩的概率为$\frac{4}{5}$，第三、第四门学科取得优秀成绩的概率分别为m，n（m＞n），且不同学科是否取得优秀成绩相互独立，记ξ为该同学取得优秀成绩的课程数，其分布列为如下表：
（1）求该生至少有1门课程取得优秀成绩的概率；
（2）求m，n的值；
（3）求数学期望Eξ．
| ξ | 0 | 1 | 2 | 3 | 4 |
| p | $\frac{1}{120}$ | x | y | z | $\frac{1}{5}$ |
（2）求m，n的值；
（3）求数学期望Eξ．
5．有2人从一座6层大楼的底层进入电梯，假设每个人自第二层开始在每一层离开电梯是等可能的，则该2人在不同层离开电梯的概率是（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{5}$ | C． | $\frac{4}{5}$ | D． | $\frac{5}{6}$ |
12．直线（cos$\frac{π}{6}$）x+（sin$\frac{π}{6}$）y+2=0的倾斜角为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{5π}{6}$ | C． | $\frac{π}{3}$ | D． | $\frac{2π}{3}$ |
2．已知函数$f（x）=\left\{\begin{array}{l}lo{g_2}x+2，x＞0\\{3^x}，x≤0\end{array}\right.$，则$f[f（\frac{1}{8}）]$的值（ ）
| A． | 3 | B． | $\frac{1}{3}$ | C． | -3 | D． | $-\frac{1}{3}$ |
9．若点$M（a，\frac{1}{b}）$和$N（b，\frac{1}{c}）$都在直线l：x+y=1上，又点P$（c，\frac{1}{a}）$和点$Q（\frac{1}{c}，b）$，则（ ）
| A． | 点P和Q都不在直线l上 | B． | 点P和Q都在直线l上 | ||
| C． | 点P在直线l上且Q不在直线l上 | D． | 点P不在直线l上且Q在直线l上 |