题目内容
数列{an}的前n项和为Sn,若数列{an}的各项按如下规律排列: ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, …,
…, ,
, ,…,
,…, ,…有如下运算和结论:
,…有如下运算和结论:
①a24= ;
;
②数列a1,a2+a3,a4+a5+a6,a7+a8+a9+a10,…是等比数列;
③数列a1,a2+a3,a4+a5+a6,a7+a8+a9+a10,…的前n项和为Tn= ;
;
④若存在正整数k,使Sk<10,Sk+1≥10,则ak= .
.
其中正确的结论是________.(将你认为正确的结论序号都填上)
①③④
分析:①前24项构成的数列是: ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,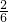 ,…,
,…, ,
,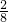 ,
, ,故a24=
,故a24= ;
;
②数列a1,a2+a3,a4+a5+a6,a7+a8+a9+a10,…是 ,1,
,1, ,2,…
,2,… ,由等差数列定义知:数列a1,a2+a3,a4+a5+a6,a7+a8+a9+a10,…是等差数列;
,由等差数列定义知:数列a1,a2+a3,a4+a5+a6,a7+a8+a9+a10,…是等差数列;
③数列a1,a2+a3,a4+a5+a6,a7+a8+a9+a10,…是等差数列,所以由等差数列前n项和公式可知:Tn= ;
;
④由③知Sk<10,Sk+1≥10,即: ,
, ,故ak=
,故ak= .
.
解答:①前24项构成的数列是: ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,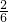 ,…,
,…, ,
,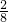 ,
, ,
,
∴a24= ,故①正确;
,故①正确;
②数列a1,a2+a3,a4+a5+a6,a7+a8+a9+a10,…是 ,1,
,1, ,2,…
,2,… ,
,
由等差数列定义 =
= (常数)
(常数)
所以数列a1,a2+a3,a4+a5+a6,a7+a8+a9+a10,…是等差数列,故②不正确.
③∵数列a1,a2+a3,a4+a5+a6,a7+a8+a9+a10,…是等差数列,
所以由等差数列前n项和公式可知:Tn= ,故③正确;
,故③正确;
④由③知Sk<10,Sk+1≥10,
即: ,
, ,∴k=7,ak=
,∴k=7,ak= .故④正确.
.故④正确.
故答案为:①③④.
点评:本题主要考查探究数列的规律,转化数列,构造数列来研究相应数列通项和前n项和问题,这种题难度较大,必须从具体到一般地静心研究,再推广到一般得到结论.
分析:①前24项构成的数列是:
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,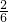 ,…,
,…, ,
,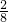 ,
, ,故a24=
,故a24= ;
;②数列a1,a2+a3,a4+a5+a6,a7+a8+a9+a10,…是
 ,1,
,1, ,2,…
,2,… ,由等差数列定义知:数列a1,a2+a3,a4+a5+a6,a7+a8+a9+a10,…是等差数列;
,由等差数列定义知:数列a1,a2+a3,a4+a5+a6,a7+a8+a9+a10,…是等差数列;③数列a1,a2+a3,a4+a5+a6,a7+a8+a9+a10,…是等差数列,所以由等差数列前n项和公式可知:Tn=
 ;
;④由③知Sk<10,Sk+1≥10,即:
 ,
, ,故ak=
,故ak= .
.解答:①前24项构成的数列是:
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
,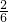 ,…,
,…, ,
,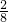 ,
, ,
,∴a24=
 ,故①正确;
,故①正确;②数列a1,a2+a3,a4+a5+a6,a7+a8+a9+a10,…是
 ,1,
,1, ,2,…
,2,… ,
,由等差数列定义
 =
= (常数)
(常数)所以数列a1,a2+a3,a4+a5+a6,a7+a8+a9+a10,…是等差数列,故②不正确.
③∵数列a1,a2+a3,a4+a5+a6,a7+a8+a9+a10,…是等差数列,
所以由等差数列前n项和公式可知:Tn=
 ,故③正确;
,故③正确;④由③知Sk<10,Sk+1≥10,
即:
 ,
, ,∴k=7,ak=
,∴k=7,ak= .故④正确.
.故④正确.故答案为:①③④.
点评:本题主要考查探究数列的规律,转化数列,构造数列来研究相应数列通项和前n项和问题,这种题难度较大,必须从具体到一般地静心研究,再推广到一般得到结论.

练习册系列答案
相关题目