题目内容
已知a,b为正数,n∈N*,证明不等式: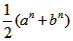 ≤
≤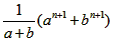 。
。
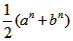 ≤
≤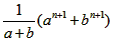 。
。证明:∵a,b为正数,∴不等式等价于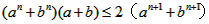
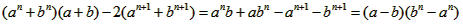
当a≥b时,a-b≥0,an≥bn,即bn-an≤0,∴(a-b)( bn-an)≤0,
当a<b时,a-b<0,an<bn,即bn-an>0,∴(a-b)( bn-an)<0,
因此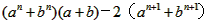 ≤0
≤0
即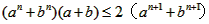
∴原不等式成立。
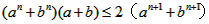
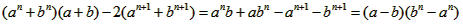
当a≥b时,a-b≥0,an≥bn,即bn-an≤0,∴(a-b)( bn-an)≤0,
当a<b时,a-b<0,an<bn,即bn-an>0,∴(a-b)( bn-an)<0,
因此
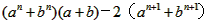 ≤0
≤0即
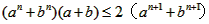
∴原不等式成立。

练习册系列答案
 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
已知a、b、m、n、x、y均为正数,且a≠b,若a、m、b、x成等差数列,a、n、b、y成等比数列,则有( )
| A、m>n,x>y | B、m>n,x<y | C、m<n,x<y | D、m<n,x>y |