题目内容
设奇函数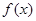 在
在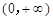 上为增函数,且
上为增函数,且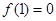 ,则不等式
,则不等式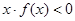 的解集为( )
的解集为( )
A.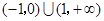 | B.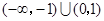 |
C.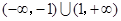 | D.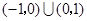 |
D
解析试题分析:因为奇函数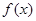 在
在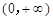 上为增函数,所以
上为增函数,所以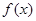 在
在 上也是增函数,且
上也是增函数,且 ,从而
,从而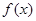 在定义域上的大致图象为:所以
在定义域上的大致图象为:所以 的解集为:
的解集为: ,故选D.
,故选D.
考点:函数的奇偶性与单调性.

练习册系列答案
相关题目
下列函数中,满足“ ”的单调递增函数是( )
”的单调递增函数是( )
A. | B.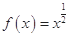 | C.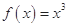 | D.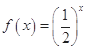 |
若奇函数 在(0,+∞)上是增函数,又
在(0,+∞)上是增函数,又 ,则
,则 的解集为( ).
的解集为( ).
| A.(-3,0)∪(3,+∞) | B.(-3,0)∪(0,3) |
| C.(-∞,-3)∪(3,+∞) | D.(-∞,-3)∪(0,3) |
设奇函数 在
在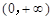 上为增函数,且
上为增函数,且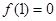 ,则不等式
,则不等式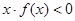 的解集为( )
的解集为( )
A. | B.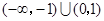 |
C. | D.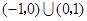 |
关于x的方程 ,在
,在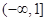 上有解,则实数a的取值范围是( )
上有解,则实数a的取值范围是( )
A.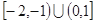 | B.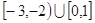 |
C.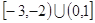 | D. |
设计下列函数求值算法程序时需要运用条件语句的函数为( ).
A. |
B. |
C. |
D. |
已知函数 ,且
,且 ,则( )
,则( )
A. | B. | C. | D. |
 ,则函数g(x)=f(x)-|lgx|的零点个数是( )
,则函数g(x)=f(x)-|lgx|的零点个数是( ) 为某一个三角形的边长,则称
为某一个三角形的边长,则称 为“
为“ 三角函数”,已知函数
三角函数”,已知函数 为“
为“


