题目内容
(本小题满分12分)
已知函数![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(I)求a,b的值;
(II)如果当x>0,且![]() 时,
时,![]() ,求k的取值范围.
,求k的取值范围.
请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,则按所做的第一题记分.做答时用2B铅笔在答题卡上把所选题目对应题号下方的方框涂黑.
解:
(Ⅰ)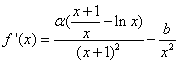
由于直线![]() 的斜率为
的斜率为![]() ,且过点
,且过点![]() ,故
,故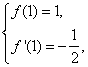 即
即
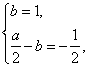 解得
解得![]() ,
,![]() .
.
(Ⅱ)由(Ⅰ)知![]() ,所以
,所以
![]() .
.
考虑函数![]()
![]()
![]() ,则
,则
![]() .
.
(i)设![]() ,由
,由![]() 知,当
知,当![]() 时,
时,![]() .而
.而![]() ,故
,故
当![]() 时,
时,![]() ,可得
,可得![]() ;
;
当x![]() (1,+
(1,+![]() )时,h(x)<0,可得
)时,h(x)<0,可得![]() h(x)>0
h(x)>0
从而当x>0,且x![]() 1时,f(x)-(
1时,f(x)-(![]() +
+![]() )>0,即f(x)>
)>0,即f(x)>![]() +
+![]() .
.
(ii)设0<k<1.由于当x![]() (1,
(1,![]() )时,(k-1)(x2 +1)+2x>0,故
)时,(k-1)(x2 +1)+2x>0,故![]() (x)>0,而
(x)>0,而
h(1)=0,故当x![]() (1,
(1,![]() )时,h(x)>0,可得
)时,h(x)>0,可得![]() h(x)<0,与题设矛盾.
h(x)<0,与题设矛盾.
(iii)设k![]() 1.此时
1.此时![]() (x)>0,而h(1)=0,故当x
(x)>0,而h(1)=0,故当x![]() (1,+
(1,+![]() )时,h(x)>0,可得
)时,h(x)>0,可得![]() h(x)<0,与题设矛盾.
h(x)<0,与题设矛盾.
综合得,k的取值范围为(-![]() ,0]
,0]
解:(2)由(1)知![]() .
.
故要证:![]() 只需证
只需证![]()
为去分母,故分x>1与0<x<1两种情况讨论:
当x>1时,需证![]()
即![]() 即需证
即需证![]() . (1)
. (1)
设![]() ,则
,则![]()
由x>1得![]() ,所以
,所以![]() 在(1,+
在(1,+![]() )上为减函数.又因g(1)=0
)上为减函数.又因g(1)=0
所以 当x>1时 g(x)<0 即(1)式成立.
同理0<x<1时,需证![]() (2)
(2)
而由0<x<1得![]() ,所以
,所以![]() 在(0,1)上为增函数.又因g(1)=0
在(0,1)上为增函数.又因g(1)=0
所以 当0<x<1时 g(x)<0 即(2)式成立.
综上所证,知要证不等式成立.
点评:抓住基本思路,去分母化简问题,不可死算.
