题目内容
设函数f(x)=ln(x+a)+x2,
(Ⅰ)若当x=-1时f(x)取得极值,求a的值,并讨论f(x)的单调性;
(Ⅱ)若f(x)存在极值,求a的取值范围,并证明所有极值之和大于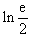 。
。
(Ⅰ)若当x=-1时f(x)取得极值,求a的值,并讨论f(x)的单调性;
(Ⅱ)若f(x)存在极值,求a的取值范围,并证明所有极值之和大于
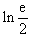 。
。 解:(Ⅰ)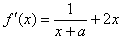 ,
,
依题意有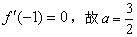 ,
,
从而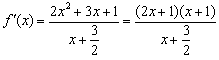 ,
,
f(x)的定义域为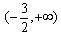 ,
,
当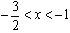 时,f′(x)>0;当
时,f′(x)>0;当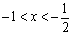 时,f′(x)<0;当
时,f′(x)<0;当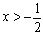 时,f′(x)>0,
时,f′(x)>0,
从而,f(x)分别在区间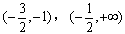 单调增加,在区间
单调增加,在区间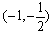 单调减少。
单调减少。
(Ⅱ)f(x)的定义域为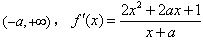 ,
,
方程 ,
,
(ⅰ)若△<0,即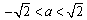 ,在f(x)的定义域内f′(x)>0,故f(x)无极值;
,在f(x)的定义域内f′(x)>0,故f(x)无极值;
(ⅱ)若△=0,则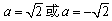 ,
,
若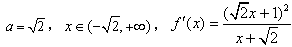 ,
,
当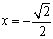 时,f′(x)=0,当
时,f′(x)=0,当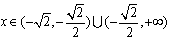 时,f′(x)>0,所以f(x)无极值;
时,f′(x)>0,所以f(x)无极值;
若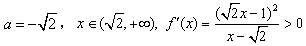 ,f(x)也无极值;
,f(x)也无极值;
(ⅲ)若△>0,即 ,
,
则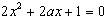 有两个不同的实根
有两个不同的实根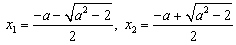 ,
,
当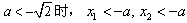 ,
,
从而f′(x)在f(x)的定义域内没有零点,故f(x)无极值;
当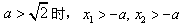 ,
,
f′(x)在f(x)的定义域内有两个不同的零点,
由极值判别方法知f(x)在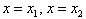 取得极值;
取得极值;
综上,f(x)存在极值时,a的取值范围为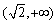 ;
;
f(x)的极值之和为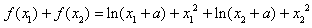
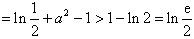 。
。
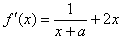 ,
,依题意有
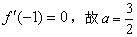 ,
,从而
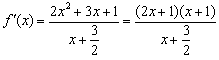 ,
,f(x)的定义域为
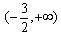 ,
,当
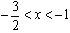 时,f′(x)>0;当
时,f′(x)>0;当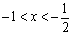 时,f′(x)<0;当
时,f′(x)<0;当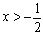 时,f′(x)>0,
时,f′(x)>0,从而,f(x)分别在区间
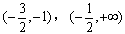 单调增加,在区间
单调增加,在区间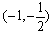 单调减少。
单调减少。 (Ⅱ)f(x)的定义域为
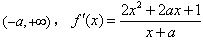 ,
,方程
 ,
,(ⅰ)若△<0,即
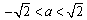 ,在f(x)的定义域内f′(x)>0,故f(x)无极值;
,在f(x)的定义域内f′(x)>0,故f(x)无极值;(ⅱ)若△=0,则
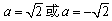 ,
,若
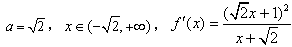 ,
,当
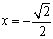 时,f′(x)=0,当
时,f′(x)=0,当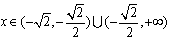 时,f′(x)>0,所以f(x)无极值;
时,f′(x)>0,所以f(x)无极值;若
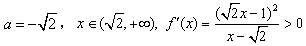 ,f(x)也无极值;
,f(x)也无极值;(ⅲ)若△>0,即
 ,
,则
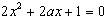 有两个不同的实根
有两个不同的实根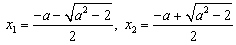 ,
,当
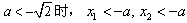 ,
,从而f′(x)在f(x)的定义域内没有零点,故f(x)无极值;
当
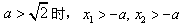 ,
,f′(x)在f(x)的定义域内有两个不同的零点,
由极值判别方法知f(x)在
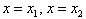 取得极值;
取得极值;综上,f(x)存在极值时,a的取值范围为
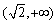 ;
;f(x)的极值之和为
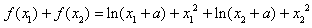
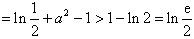 。
。
练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目