题目内容
线段AB与CD互相垂直且平分于点O,｜AB｜＝2A,|CD|＝２B,动点P满足｜PA｜·｜PB｜＝｜PC｜·｜PD｜,求动点P的轨迹方程.
解:以AB的中点O为原点，直线AB为x轴建立直角坐标系，如右图所示.设P(x，y)，又A(-a，0)、B(a，0)、C(0，-b)、D(0，b)，
由题设,知｜PA｜·｜PB｜＝｜PC｜·｜PD｜.
∴
化简，得x2－y2＝
为所求.(证明略).
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
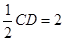，点M在线段EC上且不与E、C垂合.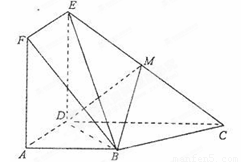
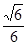时，求三棱锥M—BDE的体积.