题目内容
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,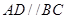 ,
,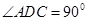 ,平面
,平面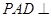 底面
底面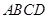 ,
,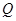 为
为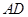 中点,M是棱PC上的点,
中点,M是棱PC上的点,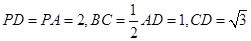 .
.

(1)若点M是棱PC的中点,求证: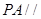 平面
平面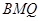 ;
;
(2)求证:平面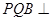 底面
底面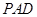 ;
;
(3)若二面角M-BQ-C为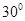 ,设PM=tMC,试确定t的值.
,设PM=tMC,试确定t的值.
(1)见解析;(2)见解析;(3)3.
【解析】
试题分析:(1)连接AC,交BQ于N,连接MN,在三角形PAC中,利用中位线定理证明PA//MN,由线线平行得线面平行;(2)证PQ⊥AD,QB⊥AD,由PQ∩BQ=Q,所以AD⊥平面PBQ,再利用线面垂直得面面垂直;(3)先证PQ⊥面ABCD,(注意此步不可省略),再以Q为原点建立空间直角坐标系,写出各点坐标及平面BQC的法向量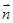 ,并设
,并设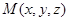 ,利用关系PM=tMC,用坐标表示出来,列方程解出
,利用关系PM=tMC,用坐标表示出来,列方程解出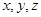 ,并得
,并得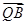 ,
,
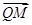 ,从而易得平面MBQ法向量为
,从而易得平面MBQ法向量为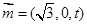 ,再由数量积运算得
,再由数量积运算得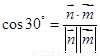 ,可得t值.
,可得t值.
试题解析:证明:(1)连接AC,交BQ于N,连接MN. 1分
∵BC∥AD且BC=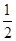 AD,即BC
AD,即BC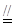 AQ.∴四边形BCQA为平行四边形,且N为AC中点,
AQ.∴四边形BCQA为平行四边形,且N为AC中点,
又∵点M是棱PC的中点,∴ MN // PA 2分
∵ MN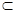 平面MQB,PA
平面MQB,PA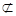 平面MQB,
3分
平面MQB,
3分
∴ PA // 平面MBQ. 4分
(2)∵AD // BC,BC=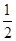 AD,Q为AD的中点,∴四边形BCDQ为平行四边形,∴CD // BQ . 6分
AD,Q为AD的中点,∴四边形BCDQ为平行四边形,∴CD // BQ . 6分
∵∠ADC=90° ∴∠AQB=90° 即QB⊥AD.
又∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD, 7分
∴BQ⊥平面PAD. 8分
∵BQ 平面PQB,∴平面PQB⊥平面PAD.
9分
平面PQB,∴平面PQB⊥平面PAD.
9分
另证:AD // BC,BC= AD,Q为AD的中点∴ BC // DQ 且BC= DQ,
AD,Q为AD的中点∴ BC // DQ 且BC= DQ,
∴ 四边形BCDQ为平行四边形,∴CD // BQ .
∵ ∠ADC=90° ∴∠AQB=90° 即QB⊥AD. 6分
∵ PA=PD, ∴PQ⊥AD. 7分
∵ PQ∩BQ=Q,∴AD⊥平面PBQ. 8分
∵ AD 平面PAD,∴平面PQB⊥平面PAD.
9分
平面PAD,∴平面PQB⊥平面PAD.
9分
(Ⅲ)∵PA=PD,Q为AD的中点, ∴PQ⊥AD.
∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD, ∴PQ⊥平面ABCD. 10分
(不证明PQ⊥平面ABCD直接建系扣1分)
如图,以Q为原点建立空间直角坐标系.
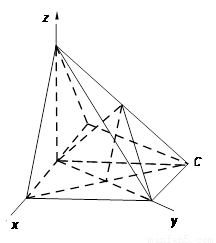
则平面BQC的法向量为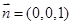 ;
;
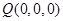 ,
,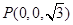 ,
,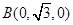 ,
,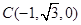 . 11分
. 11分
设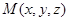 ,
,
则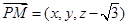 ,
,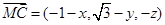 ,∵
,∵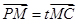 ,
,
∴ 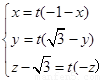 , ∴
, ∴ 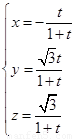 ,
12分
,
12分
在平面MBQ中,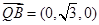 ,
,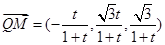 ,
,
∴ 平面MBQ法向量为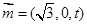 .
13分
.
13分
∵二面角M-BQ-C为30°, 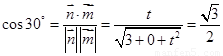 ,∴
,∴
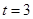 . 14分
. 14分
考点:1、线面平行的判定定理;2、面面垂直的判定定理;3、利用空间直角坐标系解决问题.

 阅读快车系列答案
阅读快车系列答案 如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=3,AD=2,PA=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=3,AD=2,PA=2,PD=2 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,点A在PD上的射影为点G,点E在AB上,平面PEC⊥平面PDC.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,点A在PD上的射影为点G,点E在AB上,平面PEC⊥平面PDC. 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠BCD=120°,BC⊥AB,CD⊥AD,BC=CD=PA=a,
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠BCD=120°,BC⊥AB,CD⊥AD,BC=CD=PA=a, 如图,在四棱锥P-ABCD中,底面是边长为a的菱形,∠ABC=60°PD⊥面ABCD,PC=a,E为PB中点
如图,在四棱锥P-ABCD中,底面是边长为a的菱形,∠ABC=60°PD⊥面ABCD,PC=a,E为PB中点 (2008•武汉模拟)如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,BC∥AD,且∠BAD=90°,又PA⊥底面ABCD,BC=AB=PA=1,AD=2.
(2008•武汉模拟)如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,BC∥AD,且∠BAD=90°,又PA⊥底面ABCD,BC=AB=PA=1,AD=2.