题目内容
设平面向量 ,
, .
.(I)当m,n∈{-2,-1,1,2}时.记“
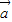 ⊥
⊥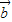 ”为事件A,求事件A发生的概率;
”为事件A,求事件A发生的概率;(II)当m∈[-1,2],n∈[-1,1]时,记“
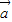 与
与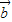 所成角为钝角”为事件B,求事件B发生的概率.
所成角为钝角”为事件B,求事件B发生的概率.
【答案】分析:(1)首先求出有序数组(m,n)的所有可能结果,然后找出满足条件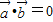 的所有数组,运用古典概型求事件A发生的概率;
的所有数组,运用古典概型求事件A发生的概率;
(2)根据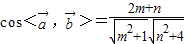 知,
知,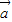 与
与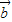 所成角为钝角,则2m+n<0,除去使余弦值为-1的角,结合m∈[-1,2],n∈[-1,1]求出m和n所满足的条件,运用几何概型求事件B发生的概率.
所成角为钝角,则2m+n<0,除去使余弦值为-1的角,结合m∈[-1,2],n∈[-1,1]求出m和n所满足的条件,运用几何概型求事件B发生的概率.
解答: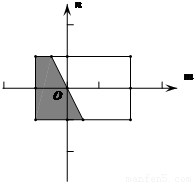 解:(I)有序数组(m,n)的所有可能结果为:(-2,-2),(-2,-1),(-2,1),(-2,2),
解:(I)有序数组(m,n)的所有可能结果为:(-2,-2),(-2,-1),(-2,1),(-2,2),
(-1,-2),(-1,-1),(-1,1),(-1,2),(1,-2),(1,-1),(1,1),(1,2),(2,-2),
(2,-1),(2,1),(2,2)共有16种.
使得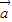 ⊥
⊥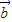 成立的( m,n ),满足:2m+n=0,n=-2m
成立的( m,n ),满足:2m+n=0,n=-2m
事件A有(-1,2),(1,-2)有2种.
故所求的概率为: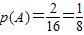 .
.
(II)使得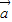 与
与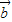 所成角为钝角成立的( m,n )满足:2m+n<0,且mn≠2.
所成角为钝角成立的( m,n )满足:2m+n<0,且mn≠2.
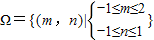 ,
,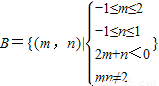 ,区域如图所示,
,区域如图所示,
∴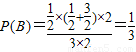 .
.
点评:本题考查了运用数量积判断两个向量的垂直关系,考查了古典概型和几何概型,考查了数学转化思想,注意(2)中的测度比是面积比,该题为中档难度的题型.
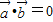 的所有数组,运用古典概型求事件A发生的概率;
的所有数组,运用古典概型求事件A发生的概率;(2)根据
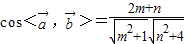 知,
知,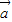 与
与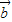 所成角为钝角,则2m+n<0,除去使余弦值为-1的角,结合m∈[-1,2],n∈[-1,1]求出m和n所满足的条件,运用几何概型求事件B发生的概率.
所成角为钝角,则2m+n<0,除去使余弦值为-1的角,结合m∈[-1,2],n∈[-1,1]求出m和n所满足的条件,运用几何概型求事件B发生的概率.解答:
 解:(I)有序数组(m,n)的所有可能结果为:(-2,-2),(-2,-1),(-2,1),(-2,2),
解:(I)有序数组(m,n)的所有可能结果为:(-2,-2),(-2,-1),(-2,1),(-2,2),(-1,-2),(-1,-1),(-1,1),(-1,2),(1,-2),(1,-1),(1,1),(1,2),(2,-2),
(2,-1),(2,1),(2,2)共有16种.
使得
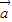 ⊥
⊥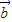 成立的( m,n ),满足:2m+n=0,n=-2m
成立的( m,n ),满足:2m+n=0,n=-2m事件A有(-1,2),(1,-2)有2种.
故所求的概率为:
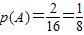 .
.(II)使得
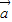 与
与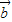 所成角为钝角成立的( m,n )满足:2m+n<0,且mn≠2.
所成角为钝角成立的( m,n )满足:2m+n<0,且mn≠2.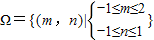 ,
,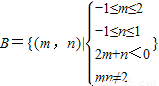 ,区域如图所示,
,区域如图所示,∴
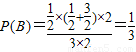 .
.点评:本题考查了运用数量积判断两个向量的垂直关系,考查了古典概型和几何概型,考查了数学转化思想,注意(2)中的测度比是面积比,该题为中档难度的题型.

练习册系列答案
相关题目
 ,
,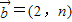 .
.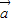 ⊥
⊥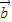 ”为事件A,求事件A发生的概率;
”为事件A,求事件A发生的概率; 与
与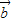 所成角为钝角”为事件B,求事件B发生的概率.
所成角为钝角”为事件B,求事件B发生的概率.