题目内容
在△ABC中,A,B,C所对的边是 .
.
(1)若sin(B-A)=cosC,求A,C;
(2)若a=2,当sinA+sinB取最大值时,求△ABC的面积.
解:(I)由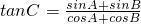 .得sin(C-A)=sin(B-C),∴C-A=B-C或C-A=π-(B-C)(不合题意,舍去),∴
.得sin(C-A)=sin(B-C),∴C-A=B-C或C-A=π-(B-C)(不合题意,舍去),∴ .…(4分)
.…(4分)
由sin(B-A)=cosC,得 ,
,
∴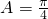 .…(6分)
.…(6分)
(Ⅱ)令 ,
,
∴当 时,
时, .…(9分)
.…(9分)
∴△ABC为等边三角形,…(10分)
∴ .…(12分)
.…(12分)
分析:(I)由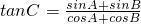 .得sin(C-A)=sin(B-C),故C-A=B-C,
.得sin(C-A)=sin(B-C),故C-A=B-C, ,由sin(B-A)=cosC,求得
,由sin(B-A)=cosC,求得 ,
,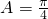 .
.
(Ⅱ)令 ,故当
,故当 时,
时, ,可得△ABC为等边三角形,从而求得它的面积.
,可得△ABC为等边三角形,从而求得它的面积.
点评:本题主要考查三角函数的恒等变换及化简求值,三角形中的几何计算,属于中档题.
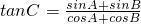 .得sin(C-A)=sin(B-C),∴C-A=B-C或C-A=π-(B-C)(不合题意,舍去),∴
.得sin(C-A)=sin(B-C),∴C-A=B-C或C-A=π-(B-C)(不合题意,舍去),∴ .…(4分)
.…(4分)由sin(B-A)=cosC,得
 ,
,∴
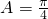 .…(6分)
.…(6分)(Ⅱ)令
 ,
,∴当
 时,
时, .…(9分)
.…(9分)∴△ABC为等边三角形,…(10分)
∴
 .…(12分)
.…(12分)分析:(I)由
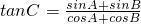 .得sin(C-A)=sin(B-C),故C-A=B-C,
.得sin(C-A)=sin(B-C),故C-A=B-C, ,由sin(B-A)=cosC,求得
,由sin(B-A)=cosC,求得 ,
,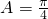 .
.(Ⅱ)令
 ,故当
,故当 时,
时, ,可得△ABC为等边三角形,从而求得它的面积.
,可得△ABC为等边三角形,从而求得它的面积.点评:本题主要考查三角函数的恒等变换及化简求值,三角形中的几何计算,属于中档题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
在△ABC中,∠A、∠B、∠C所对的边长分别是a、b、c.满足2acosC+ccosA=b.则sinA+sinB的最大值是( )
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|