题目内容
求一边和这边所对的角的大小均为定值的三角形顶点的轨迹方程.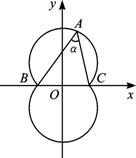
解析:建立如图所示坐标系,设B(-a,0)、C(a,0)、A(x,y),则
(1)当α=90°时,AB、AC不垂直于x轴,
∴kAB、kAC存在,且kAB·kAC=-1.
∴![]() =-1,即x2+y2=a2.但y≠0,
=-1,即x2+y2=a2.但y≠0,
∴所求的轨迹方程是x2+y2=a2(y≠0).
(2)当α≠90°时,设tanα=m,m是定值,
①若点A在x轴上方,则tanα=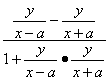 =m,化简得x2+(y-
=m,化简得x2+(y-![]() )2=a2(1+
)2=a2(1+![]() ),其中y>0.
),其中y>0.
②若点A在x轴下方,则tanα=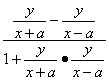 =m,化简得x2+(y+
=m,化简得x2+(y+![]() )2=a2(1+
)2=a2(1+![]() ),其中y<0.
),其中y<0.
综上所述,所求三角形顶点的轨迹方程为x2+y2=a2(y≠0)或x2+(y-![]() )2=a2(1+
)2=a2(1+![]() )(y>0)或 x2+(y+
)(y>0)或 x2+(y+![]() )2=a2(1+
)2=a2(1+![]() )(y<0).
)(y<0).

练习册系列答案
相关题目