题目内容
己知函数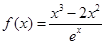 .
.
(I)求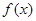 的极大值和极小值;
的极大值和极小值;
(II)当 时,
时, 恒成立,求
恒成立,求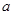 的取值范围.
的取值范围.
【答案】
(I)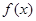 的极大值为
的极大值为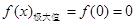 和
和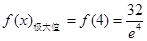 ;
;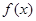 的极小值为
的极小值为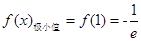 .(II)
.(II)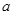 的取值范围是
的取值范围是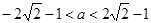 .
.
【解析】
试题分析:(I) 易知函数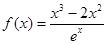 定义域为
定义域为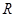 ,在
,在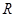 上讨论
上讨论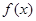 的极值先求导
的极值先求导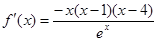 ,列出
,列出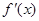 的正负表,再根据函数的单调性和极值与倒数的关系即可求出极值.
的正负表,再根据函数的单调性和极值与倒数的关系即可求出极值.
(II) 本题是不等式恒成立求参数范围问题,一般思路是化简-分类讨论,但本题中化简后为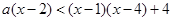 ,如果用
,如果用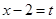 即
即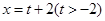 换元后为
换元后为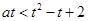 讨论起来更简单.分别讨论
讨论起来更简单.分别讨论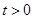 时,化简为
时,化简为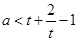 ;‚
;‚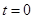 时,恒成立;‚
时,恒成立;‚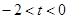 时化简为
时化简为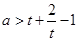 三种情况,运用均值不等式求出范围即可.
三种情况,运用均值不等式求出范围即可.
试题解析:(I) 函数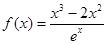 ,知定义域为
,知定义域为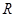 ,
,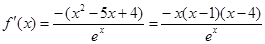 .
.
所以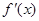 的变化情况如下:
的变化情况如下:
|
|
|
|
|
|
|
|
|
|
|
+ |
0 |
- |
0 |
+ |
0 |
- |
|
|
递增 |
极大值 |
递减 |
极小值 |
递增 |
极大值 |
递减 |
所以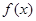 的极大值为
的极大值为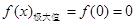 和
和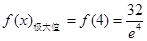 ;
;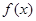 的极小值为
的极小值为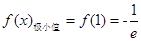 .
.
(II) 当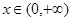 时,
时,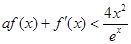 恒成立,化简为
恒成立,化简为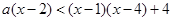 ,令
,令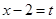
则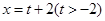 ,代入化简为
,代入化简为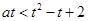 .当
.当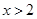 时,即
时,即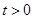 ,
,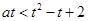 等价于
等价于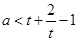
由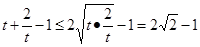 ,当且仅当
,当且仅当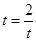 时,即
时,即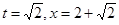 等号成立.所以
等号成立.所以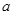 的取子范围是
的取子范围是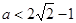 ;‚当
;‚当 时,即
时,即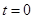 ,不等式
,不等式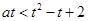 恒成立;ƒ当
恒成立;ƒ当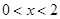 时,即
时,即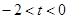 ,
,
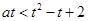 等价于
等价于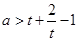 由
由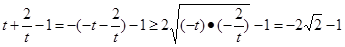 ,当且仅当
,当且仅当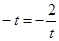 时,即
时,即 等号成立.所以
等号成立.所以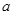 的取子范围是
的取子范围是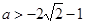 ;综上
;综上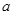 的取值范围是
的取值范围是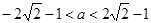 .
.
考点:1.极值的求法;2.含参不等式恒成立问题.

练习册系列答案
相关题目
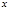
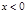
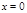
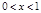
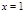
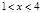
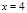
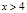
 给出下列5个命题:
给出下列5个命题: