题目内容
“对任意的正整数n,不等式nlga<(n+1)lgaa(a>0)都成立”的一个充分不必要条件是
- A.0<a<1
- B.

- C.0<a<2
- D.
 或a>1
或a>1
B
分析:原不等式等价于a(n+1)lga-nlga>0,当a>1时lga>0,a(n+1)>n,a(n+1)lga-nlga>0成立,当0<a<1时lga<0,要使a(n+1)lga-nlga>0成立,只需a(n+1)-n<0成立,即a<n/(n+1),由此知所以0<a< ,是原不等式成立的充分不必要条件.
,是原不等式成立的充分不必要条件.
解答:原不等式等价于a(n+1)lga-nlga>0,
当a>1时lga>0,a(n+1)>n,a(n+1)lga-nlga>0成立,
当0<a<1时lga<0,要使a(n+1)lga-nlga>0成立,
只需a(n+1)-n<0成立,即a<n/(n+1),
由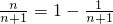 ,知
,知 最小值为
最小值为 ,
,
所以0<a< ,
,
所以0<a< 或a>1是原不等式成立的充要条件
或a>1是原不等式成立的充要条件
0<a< 是原不等式成立的充分不必要条件.
是原不等式成立的充分不必要条件.
故选B.
点评:本题考查充分条件、必要条件和充要条件的性质和应用,解题时要认真审题,注意不等式的合理运用.
分析:原不等式等价于a(n+1)lga-nlga>0,当a>1时lga>0,a(n+1)>n,a(n+1)lga-nlga>0成立,当0<a<1时lga<0,要使a(n+1)lga-nlga>0成立,只需a(n+1)-n<0成立,即a<n/(n+1),由此知所以0<a<
 ,是原不等式成立的充分不必要条件.
,是原不等式成立的充分不必要条件.解答:原不等式等价于a(n+1)lga-nlga>0,
当a>1时lga>0,a(n+1)>n,a(n+1)lga-nlga>0成立,
当0<a<1时lga<0,要使a(n+1)lga-nlga>0成立,
只需a(n+1)-n<0成立,即a<n/(n+1),
由
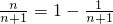 ,知
,知 最小值为
最小值为 ,
,所以0<a<
 ,
,所以0<a<
 或a>1是原不等式成立的充要条件
或a>1是原不等式成立的充要条件0<a<
 是原不等式成立的充分不必要条件.
是原不等式成立的充分不必要条件.故选B.
点评:本题考查充分条件、必要条件和充要条件的性质和应用,解题时要认真审题,注意不等式的合理运用.

练习册系列答案
相关题目
 设C1,C2,…,Cn,…是坐标平面上的一列圆,它们的圆心都在x轴的正半轴上,且都与直线
设C1,C2,…,Cn,…是坐标平面上的一列圆,它们的圆心都在x轴的正半轴上,且都与直线