Question

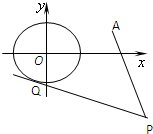已知圆O：x²+y²=1和定点A（2，1），由圆O外一点P向圆O引切线PQ，切点为Q，且满足|PQ|=|PA|．
（Ⅰ）求P点的轨迹方程；
（Ⅱ）求线段PQ长的最小值，并求此时PQ的斜率．

Answer 1

分析：（Ⅰ）利用勾股定理，结合|PQ|=|PA|，建立方程，化简可得P点的轨迹方程；
（Ⅱ）表示出线段PQ长，利用配方法可求线段PQ长的最小值，设出PQ的方程了直线与圆相切，即可并求此时PQ的斜率．

解答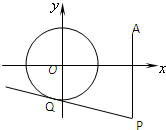：解：（Ⅰ）设P（x，y），连OP，则
∵Q为切点，∴PQ⊥OQ，
由勾股定理有|PQ|²=|OP|²-|OQ|²（2分）
又由已知|PQ|=|PA|，故|PQ|²=|PA|²．
即：（x²+y²）-1²=（x-2）²+（y-1）²．
整理得2x+y-3=0．     （4分）
（Ⅱ）由2x+y-3=0，得y=-2x+3．
∴|PQ|=

x2+y2-1

=

x2+(-2x+3)2-1

=

5x2-12x+8

=

5(x- 6 5 )2+ 4 5

故当x=

6

5

时，|PQ|min=

2

5

5

．
即线段PQ长的最小值为

2

5

5

．（8分）
此时y=

3

5

，设PQ方程为y-

3

5

=k(x-

6

5

)，即5kx-5y-6k+3=0（9分）
∵与圆相切，∴

|3-6k|

25+25k2

=1（10分）
解得k=

18±10 5

11

（12分）

点评：本题考查轨迹方程，考查直线与圆的位置关系，考查配方法的运用，考查学生的计算能力，属于中档题．