Question

已知函数f（x）=Asin（ωx+?）(A＞0，ω＞0，|?|＜

π

2

)的部分图象如图所示，若函数y=g（x）的图象与函数y=f（x）的图象关于直线x=

π

4

对称．
（1）求函数g（x）的解析式；
（2）若关于x的方程3[g（x）]²-mg（x）+1=0在区间(-

π

2

，

π

2

)上有解，求实数m的取值范围；
（3）令F（x）=f（x）+g（x），x∈[0，π]，求函数F（x）的值域．

Answer 1

分析：（1）利用函数图象先求函数的振幅和周期，再确定初相φ的值，最后利用函数图象的对称性，求得函数g（x）的解析式即可
（2）先求函数g（x）在区间(-

π

2

，

π

2

)上的值域，再将方程有解问题转化为求函数m=3[g(x)+

1 3

g(x)

]，g(x)∈(-

3

2

，1]的值域问题，利用均值定理即可求得函数值域；
（3）先利用三角变换公式将函数F（x）的解析式化简为y=Asin（ωx+φ）型函数，再利用正弦函数的图象和性质求函数值域即可

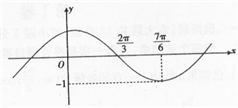
解答：解：（1）由图可知，A=1，
T=4×(

7π

6

-

2π

3

)=2π，∴ω=1，
即f(x)=sin(x+

π

3

)．
∴g(x)=f(

π

2

-x)=sin(

5π

6

-x)=sin(x+

π

6

)．
（2）∵-

π

2

＜x＜

π

2

，
∴-

π

3

＜x+

π

6

＜

2π

3

，
∴g(x)∈(-

3

2

，1]．
又3[g（x）]²-mg（x）+1=0，
∴m=3g(x)+

1

g(x)

=3[g(x)+

1 3

g(x)

]，
①当g（x）=0时，m∈φ；
②当-

3

2

＜g(x)＜0时，m=3[g(x)+

1 3

g(x)

]=-3[-g(x)+

1 3

-g(x)

]≤-3×2

1 3

=-2

3

∴m∈(-∞，-2

3

]；
③当0＜g（x）≤1时，m=3[g(x)+

1 3

g(x)

]≥3×2

1 3

=2

3

∴m∈[2

3

，+∞)．
综上，实数m的取值范围是(-∞，-2

3

]∪[2

3

，+∞)．
（3）∵F（x）=f（x）+g（x），
∴F(x)=sin(x+

π

3

)+sin(x+

π

6

)=

1+ 3

2

(sinx+cosx)=

2 + 6

2

sin(x+

π

4

)．
又x∈[0，π]，∴

π

4

≤x+

π

4

≤

5π

4

，
∴-

2

2

≤sin(x+

π

4

)≤1，
即-

1+ 3

2

≤F(x)≤

2 + 6

2

，
∴函数函数F（x）的值域为[-

1+ 3

2

，

2 + 6

2

]．

点评：本题主要考查了y=Asin（ωx+φ）型函数的图象和性质，三角变换公式在化简和求值中的应用，均值定理求函数最值的方法，属中档题