题目内容
已知函数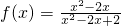 的值域A,函数g(x)=2-2x(x≤0)的值域是B,则
的值域A,函数g(x)=2-2x(x≤0)的值域是B,则
- A.A⊆B
- B.B⊆A
- C.A∩B=∅
- D.A∩B={1}
C
分析:利用函数值域求解的换元法求解A,利用函数的单调性求解B,进而求解结果.
解答:令t=x2-2x+2=(x-1)2+1≥1
 ∈[-1,1)
∈[-1,1)
故A=[-1,1)
g(x)=2-2x在(-∞,0]递减,0<2x≤1,B=[1,2)
A∩B=∅
故选C
点评:本题主要考查了函数值域求解的两种常见的方法:换元法及利用单调性求解,在求解时要注意题目中的限制条件,属于对基本知识及基本方法的考查.
分析:利用函数值域求解的换元法求解A,利用函数的单调性求解B,进而求解结果.
解答:令t=x2-2x+2=(x-1)2+1≥1
 ∈[-1,1)
∈[-1,1)故A=[-1,1)
g(x)=2-2x在(-∞,0]递减,0<2x≤1,B=[1,2)
A∩B=∅
故选C
点评:本题主要考查了函数值域求解的两种常见的方法:换元法及利用单调性求解,在求解时要注意题目中的限制条件,属于对基本知识及基本方法的考查.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目