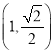题目内容
【题目】已知函数![]() .
.
(1)求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)求函数![]() 在
在![]() 上的值域;
上的值域;
(3)若存在![]() ,使得
,使得![]() 成立,求
成立,求![]() 的最大值.(其中自然常数
的最大值.(其中自然常数![]() )
)
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() 的最大值为6.
的最大值为6.
【解析】
)(1)对![]() 求导得到
求导得到![]() ,然后代入切点横坐标,得到斜率,点斜式写出切线方程,整理得答案;(2)利用导数判断出
,然后代入切点横坐标,得到斜率,点斜式写出切线方程,整理得答案;(2)利用导数判断出![]() 的单调性,根据单调性求出其最小值,并比较在两个端点时的函数值,得到最大值,从而得到答案;(3)由(2)可得
的单调性,根据单调性求出其最小值,并比较在两个端点时的函数值,得到最大值,从而得到答案;(3)由(2)可得![]() ,要使
,要使![]() 成立,且
成立,且![]() 的值最大,则
的值最大,则![]() ,
,![]() …
…![]() 的值应最小,即
的值应最小,即![]() ,
,![]() ,从而得到
,从而得到![]() ,从而得到
,从而得到![]() 的最大值为
的最大值为![]() .
.
解:(1)![]() ,
,
∴![]() ,又
,又![]() ,
,
∴![]() ,即
,即![]() 为所求切线的方程.
为所求切线的方程.
(2)![]()
令![]() ,得
,得![]() (舍去负根)
(舍去负根)
所以![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
故![]() ,
,
又因为![]() ,
,
![]() ,
,
故![]() ,
,
故![]() 时,
时,![]() .
.
(3)由(2)知,![]() 时,
时,![]() .
.
所以有![]()
而要使![]() 成立,且
成立,且![]() 的值最大,
的值最大,
则![]() ,
,![]() …
…![]() 每个的函数值应最小,
每个的函数值应最小,
即,即![]() ,
,![]() ,
,
从而得到![]() ,
,
所以![]() ,
,
所以![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目