题目内容
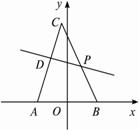
已知AB=2a,在以AB为直径的半圆上有一点C,设AB中点为O,∠AOC=60°.(1)在
 | BC |
(2)设f(θ)=PA+PB+PC,当θ为何值时f(θ)有最大值,最大值是多少?
分析:(1)在三角形中使用余弦定理求出PA、PB、PC的长度,使用二倍角公式及两角和差的三角公式进行化简.
(2)利用两角和差的三角公式进一步化简f(θ)的解析式到关于某一个角的正弦函数的形式,利用正弦函数的最值,
求出f(θ)的最大值,并求出此时θ的值.
(2)利用两角和差的三角公式进一步化简f(θ)的解析式到关于某一个角的正弦函数的形式,利用正弦函数的最值,
求出f(θ)的最大值,并求出此时θ的值.
解答:解:(1)由题意知,AB为直径的半圆的半径为a,0°<2θ<120°,∴0°≤θ≤60°,
△PAO中,由余弦定理得 PA=
=2acosθ,
同理可求得 PB=
=2asinθ,
PC=
=2asin(60°-θ),
∴PA+PB+PC=2asinθ+2acosθ+2asin(60°-θ)=2asinθ+2acosθ+2a(
cosθ-
sinθ)
=asinθ+(2+
)acosθ.
(2)f(θ)=PA+PB+PC=asinθ+(2+
)acosθ=2a
(
sinθ+
cosθ)
令cosα=
,sinα=
,则 f(θ)=2a
sin(θ+α),
取锐角α,则α=arcsin
>45°,故 当θ=90°-arcsin
时,sin(θ+α)=1取得最大值,
此时,f(θ)取最大值 2a
.
△PAO中,由余弦定理得 PA=
| a2+a2-2a•acos(180°-2θ) |
同理可求得 PB=
| a2+a2-2a•acos2θ |
PC=
| a2+a2-2a•acos(120°-2θ) |
∴PA+PB+PC=2asinθ+2acosθ+2asin(60°-θ)=2asinθ+2acosθ+2a(
| ||
| 2 |
| 1 |
| 2 |
=asinθ+(2+
| 3 |
(2)f(θ)=PA+PB+PC=asinθ+(2+
| 3 |
2+
|
| 1 | ||||
2
|
2+
| ||||
2
|
令cosα=
| 1 | ||||
2
|
2+
| ||||
2
|
2+
|
取锐角α,则α=arcsin
2+
| ||||
2
|
2+
| ||||
2
|
此时,f(θ)取最大值 2a
2+
|
点评:本题考查余弦定理、二倍角的余弦公式、两角和差的三角公式的应用,以及利用正弦函数的有界性求函数的最值,
要注意θ的范围.
要注意θ的范围.

练习册系列答案
相关题目
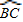 上取一点P,若∠BOP=2θ,把PA+PB+PC表示成θ的函数;
上取一点P,若∠BOP=2θ,把PA+PB+PC表示成θ的函数;