题目内容
已知函数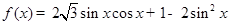 ,xÎR.
,xÎR.
(1)求函数 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)将函数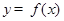 的图象上各点的纵坐标保持不变,横坐标先缩短到原来的
的图象上各点的纵坐标保持不变,横坐标先缩短到原来的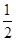 ,把所得到的图象再向左平移
,把所得到的图象再向左平移 单位,得到函数
单位,得到函数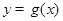 的图象,求函数
的图象,求函数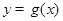 在区间
在区间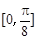 上的最小值.
上的最小值.
(1) =
= ,递增区间为
,递增区间为 ;(2)
;(2)
解析试题分析:(Ⅰ)先用正弦、余弦二倍角公式将角统一,再用化一公式,将 整理成
整理成 的形式。根据公式
的形式。根据公式 求周期,将角
求周期,将角 视为整体,代入正弦的单调增区间,即可求得
视为整体,代入正弦的单调增区间,即可求得 的范围,即
的范围,即 的单调递增区间。(Ⅱ)由(Ⅰ)知
的单调递增区间。(Ⅱ)由(Ⅰ)知 ,函数
,函数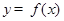 的图象上各点的纵坐标保持不变,横坐标先缩短到原来的
的图象上各点的纵坐标保持不变,横坐标先缩短到原来的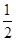 得到
得到 的图像,再向左平移
的图像,再向左平移 单位得到
单位得到 的图像。根据
的图像。根据 的范围,求整体角
的范围,求整体角 的范围,再根据正弦函数图像求
的范围,再根据正弦函数图像求 的范围,即可求得函数
的范围,即可求得函数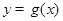 在区间
在区间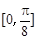 上的最小值。
上的最小值。
试题解析:解:(1)因为
= 4分
4分
函数f(x)的最小正周期为 =
= . 6分
. 6分
由
 ,
, ,
,
得f(x)的单调递增区间为 ,
,  . 8分
. 8分
(2)根据条件得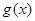 =
= ,当
,当
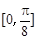 时,
时,

 ,
,
所以当x= 时,
时, . 12分
. 12分
考点:1正弦、余弦二倍角公式、化一公式;2三角函数伸缩平移变换;3三角函数的单调区间及最值;4三角函数图像。

练习册系列答案
相关题目
 (弦´矢+矢2).弧田(如图),由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.
(弦´矢+矢2).弧田(如图),由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差. ,弦长等于9米的弧田.
,弦长等于9米的弧田.
 sin x,1),n=(cos x,-y),且m⊥n.
sin x,1),n=(cos x,-y),且m⊥n.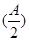 =3,且a=2,b+c=4,求△ABC的面积.
=3,且a=2,b+c=4,求△ABC的面积.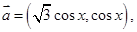 向量
向量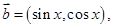 记
记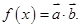
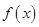 的单调递增区间;
的单调递增区间;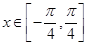 ,求函数
,求函数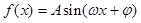 (其中
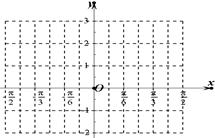
(其中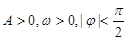 )的部分图象如图所示.
)的部分图象如图所示.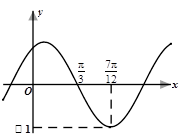
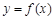 的解析式;
的解析式;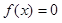 的解集.
的解集.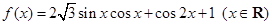 .
.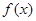 的最小正周期;
的最小正周期;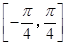 上的最小值,并写出
上的最小值,并写出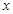 值.
值.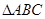 中,
中,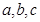 分别为角
分别为角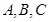 的对边,
的对边,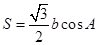
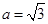 ,设角B的大小为x,用x表示c,并求c的取值范围.
,设角B的大小为x,用x表示c,并求c的取值范围. .
.
 的最小值及取最小值时
的最小值及取最小值时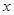 的集合;
的集合;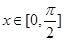 时的值域;
时的值域;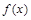 在区间
在区间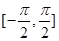 上的图像(要求列表,描点).
上的图像(要求列表,描点). .
. 的值;
的值; ,若f
,若f =2,求cos
=2,求cos 的值.
的值.