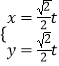Question

【题目】已知椭圆C： =1（a＞b＞0）的离心率是 ，且过点 ．直线y= x+m与椭圆C相交于A，B两点． （Ⅰ）求椭圆C的方程；
（Ⅱ）求△PAB的面积的最大值；
（Ⅲ）设直线PA，PB分别与y轴交于点M，N．判断|PM|，|PN|的大小关系，并加以证明．

Answer 1

【答案】解：（Ⅰ）设椭圆 =1（a＞b＞0）的半焦距为c，

由椭圆C的离心率是e= = = ，即a2=2b2，

将点 代入椭圆方程： ．解得 ，

∴椭圆C的方程为 ；．[（4分）]

（Ⅱ）由 ，消去y，整理得x2+ mx+m2﹣2=0．

令△=2m2﹣4（m2﹣2）＞0，解得﹣2＜m＜2．

设A（x1，y1），B（x2，y2），

则x1+x2=﹣ m，x1x2=m2﹣2．

∴丨AB丨= = ，

点 ．到直线x﹣ y+ m=0的距离为d= = ．

∴△PAB的面积S= 丨AB丨d= 丨m丨 ，

= ≤ ，

当且仅当m=± 时，S= ．

则△PAB的面积的最大值 ；

（Ⅲ）丨PM丨=丨PN丨．证明如下：

设直线PA，PB的斜率分别是k1，k1，

则k1+k2= + = ，

由（Ⅱ）得（y1﹣1）（x2﹣ ）+（y2﹣1）（x1﹣ ），

=（ x1+m﹣1）（x2﹣ ）+（ x1+m﹣1）（x1﹣ ），

= x1x2+（m﹣2）（x1+x2）﹣2 （m﹣1），

= （m2﹣2）+（m﹣2）（﹣ m）﹣2 （m﹣1）=0，

∴直线PA，PB的倾斜角互补．

∴∠1=∠2，

∴∠PMN=∠PNM．

∴丨PM丨=丨PN丨．

【解析】（Ⅰ）由椭圆的离心率公式，求得a2=2b2，将P代入椭圆方程，即可求得a和b的值；（Ⅱ）将直线方程代入椭圆方程，由△＞0，求得m的取值范围，利用韦达定理，弦长公式，根二次函数的性质，即可求得△PAB的面积的最大值；（Ⅲ）设直线PA，PB的斜率分别是k1，k1，根据韦达定理和直线的斜率公式求得k1+k2=0，则∠PMN=∠PNM，则丨PM丨=丨PN丨．
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识，掌握椭圆标准方程焦点在x轴：，焦点在y轴：．