题目内容
已知π<α+β<| 4π |
| 3 |
| π |
| 3 |
分析:把2α-β用α+β和α-β表示出来,然后根据π<α+β<
,-π<α-β<-
,求出2α-β的取值范围.
| 4π |
| 3 |
| π |
| 3 |
解答:解:可设2α-β=x(α+β)+y(α-β)
∴
解得x=
,y=
,
∴2α-β=x(α+β)+y(α-β)=
(α+β)+
(α-β)
∴-π<2α-β<
.
∴
|
解得x=
| 1 |
| 2 |
| 3 |
| 2 |
∴2α-β=x(α+β)+y(α-β)=
| 1 |
| 2 |
| 3 |
| 2 |
∴-π<2α-β<
| π |
| 6 |
点评:此题主要考查不等关系与不等式之间的关系,此题学生易错在把α和β的范围分别解出来,要注意这个问题.

练习册系列答案
相关题目
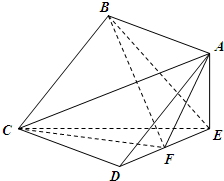 (2012•黄山模拟)如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=3,DE=4.
(2012•黄山模拟)如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=3,DE=4.