题目内容
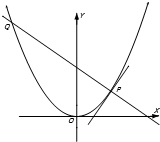 如图,P是抛物线C:y=
如图,P是抛物线C:y=| 1 | 2 |
分析:先求点P的坐标,利用导数求过点P的切线的斜率,从而可得直线l的斜率,即可求出直线l的方程.
解答:解:把x=2代入y=
x2,得y=2,
∴点P坐标为(2,2).…(3分)
由 y=
x2,①得y'=x,
∴过点P的切线的斜率k=2,…(8分)
直线l的斜率k1=-
=-
…(10分)
∴直线l的方程为y-2=-
(x-2),即x+2y-6=0…(14分)
| 1 |
| 2 |
∴点P坐标为(2,2).…(3分)
由 y=
| 1 |
| 2 |
∴过点P的切线的斜率k=2,…(8分)
直线l的斜率k1=-
| 1 |
| k |
| 1 |
| 2 |
∴直线l的方程为y-2=-
| 1 |
| 2 |
点评:本题考查利用导数研究抛物线切线的方程,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
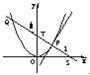 如图,P是抛物线C:y=
如图,P是抛物线C:y=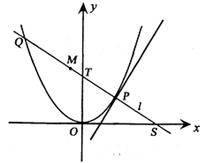 如图,P是抛物线C:y=
如图,P是抛物线C:y=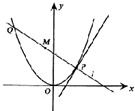 如图,P是抛物线C:y=
如图,P是抛物线C:y=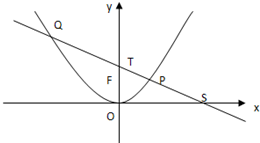 如图,P是抛物线C:x2=2y上一点,F为抛物线的焦点,直线l过点P且与抛物线交于另一点Q,已知P(x1,y1),Q(x2,y2).
如图,P是抛物线C:x2=2y上一点,F为抛物线的焦点,直线l过点P且与抛物线交于另一点Q,已知P(x1,y1),Q(x2,y2).