题目内容
若函数f(x)存在反函数f-1(x),且函数f(x)图象在点(x0,f(x0))处的切线方程为2x-y+1=0,则函数f-1(x)的图象在点(f(x0),x0)处的切线方程为
- A.2x-y+1=0
- B.x-2y-1=0
- C.x-2y+1=0
- D.2x+y-1=0
B
分析:求出直线2x-y+1=0 与直线y=x交点坐标,直线2x-y+1=0关于直线y=x对称的直线方程,即可得到所求的直线方程.
解答:由题意,直线2x-y+1=0 与直线y=x交点坐标为P(-1,-1)
直线2x-y+1=0关于直线y=x对称的直线方程为2y-x+1=0,
∴直线的斜率为 ,
,
所以所求的直线方程为
即x-2y-1=0
故选B.
点评:本题考查反函数,考查直线的方程,正确利用互为反函数的两个函数的图象关于y=x对称,属于基础题.
分析:求出直线2x-y+1=0 与直线y=x交点坐标,直线2x-y+1=0关于直线y=x对称的直线方程,即可得到所求的直线方程.
解答:由题意,直线2x-y+1=0 与直线y=x交点坐标为P(-1,-1)
直线2x-y+1=0关于直线y=x对称的直线方程为2y-x+1=0,
∴直线的斜率为
 ,
,所以所求的直线方程为

即x-2y-1=0
故选B.
点评:本题考查反函数,考查直线的方程,正确利用互为反函数的两个函数的图象关于y=x对称,属于基础题.

练习册系列答案
相关题目
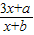 图象上有两个关于原点对称的不动点,求a,b应满足的条件;
图象上有两个关于原点对称的不动点,求a,b应满足的条件;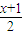 确定数列{an}的反数列,试求数列{bn}的前n项和Sn;
确定数列{an}的反数列,试求数列{bn}的前n项和Sn;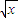 确定数列{cn}的反数列为{dn},求{dn}的通项公式;
确定数列{cn}的反数列为{dn},求{dn}的通项公式;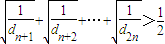 log(1-2a)对任意的正整数n恒成立,求实数a的取值范围.
log(1-2a)对任意的正整数n恒成立,求实数a的取值范围.