Question

已知抛物线C的顶点在原点,以双曲线的左准线为准线.

(1)求抛物线C的方程;

(2)A是抛物线C上任一点,A关于x轴的对称点为B,过A作抛物线的弦AP,AQ,且AP⊥AQ,是否存在常数h,使得=(h,0),且∥?若存在,求出常数h的值;若不存在,请说明理由.

Answer 1

解:(1)双曲线的左准线为x=-1,?

∴抛物线C的方程是y²=4x.                                                                              ?

(2)设A(,y₀),AP的直线方程为y-y₀=k(x-),将抛物线方程y²=4x代入AP的直线方程,得ky²-4y+4y₀-ky₀²=0,?                                                                                          ?

∴y₀+y_P=,y_P =-y₀,x_P=,?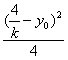

同理,y_Q=-4k-y₀,x_Q=,?

∴k_PQ===.                                                               ?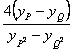

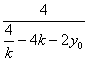∴PQ的直线方程是y+4k+y₀=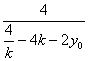·［x-］.                              ?

令y=-y₀4-4k²-2ky₀=x-,∴x=4+.

?

∴M点的坐标是(4+,-y₀).                                                                                   ?

∴存在h=4,使得=(4,0)且∥.