题目内容
设函数 的定义域为M,值域为N,那么( )
的定义域为M,值域为N,那么( )
 的定义域为M,值域为N,那么( )
的定义域为M,值域为N,那么( )| A.M={x|x≠0},N={y|y≠0} |
B.M={x|x<0且x≠-1,或x>0 ,N= ,N= y|y<0,或0<y<1,或y>1 y|y<0,或0<y<1,或y>1 |
| C.M={x|x≠0},N={y|y∈R} |
| D.M={x|x<-1,或-1<x<0,或x>0=,N={y|y≠0} |
B
分析:根据分数函数分母不等于0建立关系式即可求出函数 的定义域,求出分母的范围,根据反比例函数图象和性质可知
的定义域,求出分母的范围,根据反比例函数图象和性质可知 的值域.
的值域.
解答:解:根据题意可知 解得x≠0且x≠-1
解得x≠0且x≠-1
∴函数 的定义域为M={x|x<0且x≠-1,或x>0},
的定义域为M={x|x<0且x≠-1,或x>0},
∵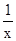 ≠0∴1+
≠0∴1+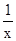 ≠1
≠1
∴根据反比例函数图象和性质可知 ≠0且y≠-1
≠0且y≠-1
∴值域N={y|y<0或0<y<1或y>1}
故选B.
 的定义域,求出分母的范围,根据反比例函数图象和性质可知
的定义域,求出分母的范围,根据反比例函数图象和性质可知 的值域.
的值域.解答:解:根据题意可知
 解得x≠0且x≠-1
解得x≠0且x≠-1∴函数
 的定义域为M={x|x<0且x≠-1,或x>0},
的定义域为M={x|x<0且x≠-1,或x>0},∵
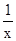 ≠0∴1+
≠0∴1+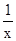 ≠1
≠1∴根据反比例函数图象和性质可知
 ≠0且y≠-1
≠0且y≠-1∴值域N={y|y<0或0<y<1或y>1}
故选B.

练习册系列答案
相关题目
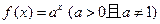 的图象上一点,数列
的图象上一点,数列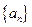 的前
的前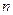 项和
项和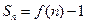 .
. 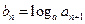 ,求数列
,求数列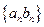 的前
的前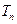 .
. ,则
,则 的取值范围是( )
的取值范围是( ) )
)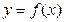 是函数
是函数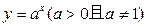 的反函数,且
的反函数,且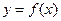 的图象过点(2,1),则
的图象过点(2,1),则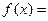 _____
_____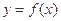 ,则
,则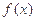 的最小正周期为 ;
的最小正周期为 ;
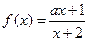 在区间
在区间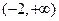 上是增函
上是增函 数,则实数
数,则实数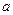 的取值范围
的取值范围  ,则
,则 = 。
= 。