题目内容
如图在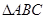 中,
中,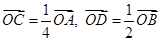 ,
,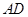 与
与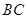 交于
交于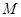 点.设
点.设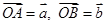 .
.
(1)用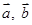 表示
表示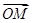 ;
;
(2) 已知线段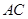 上取一点
上取一点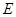 ,在线段
,在线段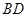 上取一点
上取一点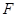 ,使
,使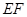 过点
过点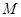 .设
.设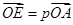 ,
,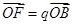 ,则
,则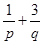 是否为定值,如果是定值,这个定值是什么?
是否为定值,如果是定值,这个定值是什么?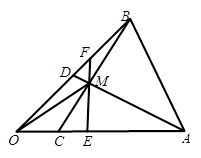
 中,
中,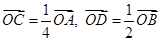 ,
,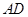 与
与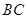 交于
交于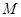 点.设
点.设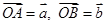 .
.(1)用
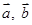 表示
表示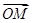 ;
;(2) 已知线段
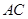 上取一点
上取一点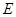 ,在线段
,在线段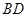 上取一点
上取一点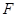 ,使
,使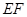 过点
过点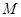 .设
.设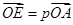 ,
,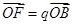 ,则
,则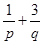 是否为定值,如果是定值,这个定值是什么?
是否为定值,如果是定值,这个定值是什么?
见解析.
第一问中,利用向量的加减法法则,可知设则

 ∵
∵ 三点共线,
三点共线,
∴ 与
与 共线,故存在实数
共线,故存在实数 ,使得
,使得 ,即
,即 ,
, ,得到
,得到
又 三点共线得到
三点共线得到
∴ 与
与 共线,同理可得
共线,同理可得 
第二问中,∵ ,
,
 ,
,
又 与
与 共线,故存在实数
共线,故存在实数 ,使得
,使得 ,即
,即 .
.
利用向量相等 ,得到结论。
,得到结论。
解:(1)设 ,则
,则 ,
,  .
.
∵ 三点共线,
三点共线,
∴ 与
与 共线,故存在实数
共线,故存在实数 ,使得
,使得 ,即
,即 ,
, ,
,
∴ ,消去
,消去 得
得 ,即
,即 . ①…………………3分
. ①…………………3分
∵ ,
, ,
,
又 三点共线
三点共线
∴ 与
与 共线,同理可得
共线,同理可得  . ②…………………………………6分
. ②…………………………………6分
联立①②,解得 .
.
故 .………………………………………………7分
.………………………………………………7分
(2) .
.
∵ ,
,
 ,
,
又 与
与 共线,故存在实数
共线,故存在实数 ,使得
,使得 ,即
,即 .
.
 ,消去
,消去 得
得 ,整理得
,整理得 .………………14分
.………………14分


 ∵
∵ 三点共线,
三点共线,∴
 与
与 共线,故存在实数
共线,故存在实数 ,使得
,使得 ,即
,即 ,
, ,得到
,得到
又
 三点共线得到
三点共线得到∴
 与
与 共线,同理可得
共线,同理可得 
第二问中,∵
 ,
, ,
,又
 与
与 共线,故存在实数
共线,故存在实数 ,使得
,使得 ,即
,即 .
.利用向量相等
 ,得到结论。
,得到结论。解:(1)设
 ,则
,则 ,
,  .
.∵
 三点共线,
三点共线,∴
 与
与 共线,故存在实数
共线,故存在实数 ,使得
,使得 ,即
,即 ,
, ,
,∴
 ,消去
,消去 得
得 ,即
,即 . ①…………………3分
. ①…………………3分∵
 ,
, ,
,又
 三点共线
三点共线∴
 与
与 共线,同理可得
共线,同理可得  . ②…………………………………6分
. ②…………………………………6分联立①②,解得
 .
. 故
 .………………………………………………7分
.………………………………………………7分(2)
 .
.∵
 ,
, ,
,又
 与
与 共线,故存在实数
共线,故存在实数 ,使得
,使得 ,即
,即 .
. ,消去
,消去 得
得 ,整理得
,整理得 .………………14分
.………………14分
练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
 的重心,过G的直线
的重心,过G的直线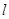 分别交AB,AC于
分别交AB,AC于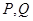 ,已知:
,已知: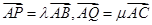 ,
,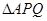 的面积分别为
的面积分别为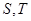 ,
,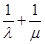 的值; (Ⅱ) 求
的值; (Ⅱ) 求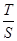 的取值范围.
的取值范围. ,则与
,则与 共线的向量为
共线的向量为



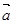 ,
,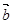 且
且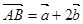 ,
,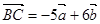 ,
,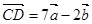 ,则一定共线的三点是
,则一定共线的三点是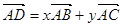 ,则x+y=__________
,则x+y=__________
 =
= ,则x+y+z=
,则x+y+z= 
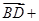
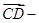
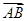 得 ( )
得 ( )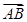
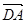
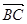
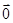
 等于( )
等于( )



 中,
中, ,延长CB到D,使
,延长CB到D,使 ,则
,则 的值是 ( )
的值是 ( )