题目内容
（本小题满分12分，（Ⅰ）小问4分，（Ⅱ）小问8分．）
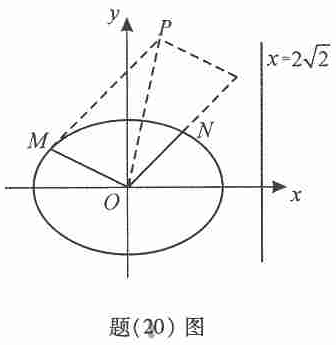
如题（20）图，椭圆的中心为原点
，离心率
，一条准线的方程为
．
（Ⅰ）求该椭圆的标准方程；
（Ⅱ）设动点
满足：
，其中
是椭圆上的点，直线
与
的斜率之积为
，问：是否存在两个定点
，使得
为定值？若存在，求的坐标；若不存在，说明理由．
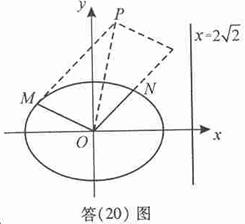
（本题12分）
解：（I）由
解得
，故椭圆的标准方程为
（II）设
，则由
得
因为点M，N在椭圆
上，所以
，
故
设
分别为直线OM，ON的斜率，由题设条件知
因此
所以
所以P点是椭圆
上的点，设该椭圆的左、右焦点为F1，F2，则由椭圆的定义|PF1|+|PF2|为定值，又因
，因此两焦点的坐标为
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
