题目内容

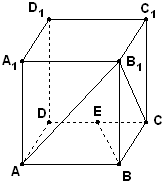精英家教网如图，四棱柱ABCD-A1B1C1D1中，底面ABCD是菱形，∠BAD=60°，AB=BB1=a，AB1=B1C=
2
a，E为CD中点．
（1）求证：AB1⊥BE；
（2）点F在线段B1C上，当
B1F
FC
为多少时，AB1∥平面BEF，并说明理由．
分析：（1）由已知中四棱柱ABCD-A1B1C1D1中，底面ABCD是菱形，∠BAD=60°，AB=BB1=a，AB1=B1C=
2
a，E为CD中点．结合直角三角形性质及等边三角形“三线合一”的性质，得到BB1⊥平面ABCD，BE⊥AB，BE⊥BB1，由线面垂直的判定定理及性质，进而得到AB1⊥BE；
（2）连接AC交BE于G，过G在平面AB1C内作GF∥AB1交B1C于F，由线面平行的判定定理可得AB1∥平面BEF，由平行线分线段成比例定理，即可求出满足条件时
B1F
FC
的值．
解答：解：（1）证明：∵AB=BB1=a，AB1=B1C=
2
a，
∴BB1⊥AB，BB1⊥BC
∴BB1⊥平面ABCD，
又∵底面ABCD是菱形，∠BAD=60°，
∴△BCD为等边三角形，
∴BE⊥CD，AB∥CD
∴BE⊥AB，BE⊥BB1
∴BE⊥平面ABB1A1，
∴BE⊥AB 1
（2）连接AC交BE于G，过G在平面AB1C内作GF∥AB1交B1C于F，
则AB1∥平面BEF，
则
B1F
FC
=
AG
GC
=2
点评：本题考查的知识点是直线与平面平行的判定，直线与平面垂直的判定，其中熟练掌握空间直线与平面的平行、垂直的判定定理、性质定理及定义是解答本题的关键．
练习册系列答案
相关题目
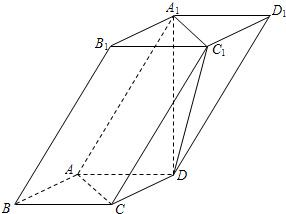精英家教网如图，四棱柱ABCD-A1B1C1D1中，A1D⊥平面ABCD，底面ABCD是边长为1的正方形，侧棱AA1=2．
（Ⅰ）求证：C1D∥平面ABB1A1；
（Ⅱ）求直线BD1与平面A1C1D所成角的正弦值；
（Ⅲ）求二面角D-A1C1-A的余弦值．
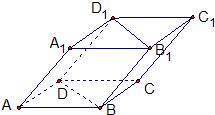精英家教网如图，四棱柱ABCD-A1B1C1D1的底面ABCD为正方形，侧棱与底面边长均为2a，且∠A1AD=∠A1AB=60°，则侧棱AA1和截面B1D1DB的距离是
 
．
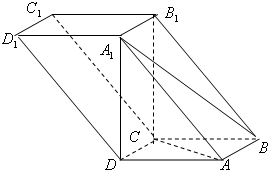精英家教网如图，四棱柱ABCD-A1B1C1D1中，A1D⊥平面ABCD，底面ABCD是边长为1的正方形，侧棱A1A=2，
（Ⅰ）证明：AC⊥A1B；
（Ⅱ）若棱AA1上存在一点P，使得
AP
=λ
PA1
，当二面角A-B1C1-P的大小为300时，求实数λ的值．
（2013•泉州模拟）如图，四棱柱ABCD-A1B1C1D1中，AA1⊥平面ABCD．
（Ⅰ）从下列①②③三个条件中选择一个做为AC⊥BD1的充分条件，并给予证明；
①AB⊥BC，②AC⊥BD；③ABCD是平行四边形．
（Ⅱ）设四棱柱ABCD-A1B1C1D1的所有棱长都为1，且∠BAD为锐角，求平面BDD1与平面BC1D1所成锐二面角θ的取值范围．
（2013•天津）如图，四棱柱ABCD-A1B1C1D1中，侧棱A1A⊥底面ABCD，AB∥DC，AB⊥AD，AD=CD=1，
AA1=AB=2，E为棱AA1的中点．
（Ⅰ）证明B1C1⊥CE；
（Ⅱ）求二面角B1-CE-C1的正弦值．
（Ⅲ）设点M在线段C1E上，且直线AM与平面ADD1A1所成角的正弦值为
2
6
，求线段AM的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网