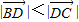题目内容
已知
，则有（ ）A．M∩N=N
B．M∩N=M
C．M∪N=N
D．M∪N=R
【答案】分析：根据题意，解x2-x≤0可得集合M，解
＜0可得集合N，分析可得N⊆M，由子集的性质可得有M∩N=N、M∪N=M成立，分析选项可得答案．
解答：解：x2-x≤0?0≤x≤1，则M={x|0≤x≤1}，
＜0?0＜x＜1，则N={x|0＜x＜1}，
有N⊆M，
则有M∩N=N，M∪N=M，
分析选项可得A符合；
故选A．
点评：本题考查集合间的关系，涉及一元二次不等式、分式不等式的解法，关键是正确解出不等式，求出集合．
＜0可得集合N，分析可得N⊆M，由子集的性质可得有M∩N=N、M∪N=M成立，分析选项可得答案．解答：解：x2-x≤0?0≤x≤1，则M={x|0≤x≤1}，
＜0?0＜x＜1，则N={x|0＜x＜1}，有N⊆M，
则有M∩N=N，M∪N=M，
分析选项可得A符合；
故选A．
点评：本题考查集合间的关系，涉及一元二次不等式、分式不等式的解法，关键是正确解出不等式，求出集合．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，则有（ ）
B．
C．
夹角为
D． 
则有（ ）
是奇函数，且
B.
，则有 （ ）
B．
C． 
D．
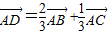，则有（ ）
