题目内容
已知椭圆方程为 .且椭圆的焦距为
.且椭圆的焦距为 ,定点
,定点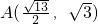 为椭圆上的点,点P为椭圆上的动点,过点P作y轴的垂线,垂足为P1,动点M满足
为椭圆上的点,点P为椭圆上的动点,过点P作y轴的垂线,垂足为P1,动点M满足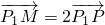
(1)求M点的轨迹T的方程;
(2)已知O(0,0)、E(2,1),试探究是否存在这样的点Q:Q是轨迹T内部的整点(平面内横、纵坐标均为整数的点称为整点),且△OEQ的面积S△OEQ=2?若存在,求出点Q的坐标,若不存在,说明理由.
解:(1)由题意可知:椭圆焦点为 .
.
|AF1|+|AF2|=2a,所以a=4,b2=a2-c2=4,所以椭圆方程为: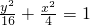 .
.
设P(x0,y0),M(x,y),由题意可得: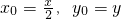 代入椭圆方程化简可得
代入椭圆方程化简可得
M点的轨迹T的方程为:x2+y2=16.
(2)连接OE,易知轨迹T上有两个点 A(-4,0),B(4,0)满足S△OEA=S△OEB=2,
分别过A、B作直线OE的两条平行线l1、l2.
∵同底等高的两个三角形的面积相等,∴符合条件的点均在直线l1、l2上.
∵ ,∴直线l1、l2的方程分别为:
,∴直线l1、l2的方程分别为: .
.
设点Q(x,y)(x,y∈Z),∵O在轨迹T内,∴x2+y2<16,
分别解 与
与 ,得
,得  ,或
,或  ,
,
∵x,y∈Z,∴x为偶数,在 上,x=-2,0,2对应的y=1,2,3
上,x=-2,0,2对应的y=1,2,3
在 上,x=-2,0,2,对应的y=-3,-2,-1,∴满足条件的点Q存在,共有6个,它们的坐标分别为:
上,x=-2,0,2,对应的y=-3,-2,-1,∴满足条件的点Q存在,共有6个,它们的坐标分别为:
(-2,1),(0,2),(2,3),(-2,-3),(0,-2),(2,-1).
分析:(1)先求得椭圆方程为,设P(x0,y0),M(x,y),由题意可得: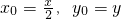 代入椭圆方程化简可得
代入椭圆方程化简可得
M点的轨迹T的方程.
(2)分别过A、B作直线OE的两条平行线l1、l2 ,符合条件的点均在直线l1、l2上,分别解 与
与 ,求得x的范围,找出其中的整数,代入直线l1、l2的方程求出y的整数值,即得点Q的坐标.
,求得x的范围,找出其中的整数,代入直线l1、l2的方程求出y的整数值,即得点Q的坐标.
点评:本题考查点轨迹方程的求法,本题考查直线和圆的位置关系,判断符合条件的点均在直线l1、l2上,是解题的关键.
 .
.|AF1|+|AF2|=2a,所以a=4,b2=a2-c2=4,所以椭圆方程为:
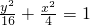 .
.设P(x0,y0),M(x,y),由题意可得:
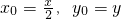 代入椭圆方程化简可得
代入椭圆方程化简可得M点的轨迹T的方程为:x2+y2=16.
(2)连接OE,易知轨迹T上有两个点 A(-4,0),B(4,0)满足S△OEA=S△OEB=2,
分别过A、B作直线OE的两条平行线l1、l2.
∵同底等高的两个三角形的面积相等,∴符合条件的点均在直线l1、l2上.
∵
 ,∴直线l1、l2的方程分别为:
,∴直线l1、l2的方程分别为: .
.设点Q(x,y)(x,y∈Z),∵O在轨迹T内,∴x2+y2<16,
分别解
 与
与 ,得
,得  ,或
,或  ,
,∵x,y∈Z,∴x为偶数,在
 上,x=-2,0,2对应的y=1,2,3
上,x=-2,0,2对应的y=1,2,3在
 上,x=-2,0,2,对应的y=-3,-2,-1,∴满足条件的点Q存在,共有6个,它们的坐标分别为:
上,x=-2,0,2,对应的y=-3,-2,-1,∴满足条件的点Q存在,共有6个,它们的坐标分别为:(-2,1),(0,2),(2,3),(-2,-3),(0,-2),(2,-1).
分析:(1)先求得椭圆方程为,设P(x0,y0),M(x,y),由题意可得:
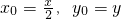 代入椭圆方程化简可得
代入椭圆方程化简可得M点的轨迹T的方程.
(2)分别过A、B作直线OE的两条平行线l1、l2 ,符合条件的点均在直线l1、l2上,分别解
 与
与 ,求得x的范围,找出其中的整数,代入直线l1、l2的方程求出y的整数值,即得点Q的坐标.
,求得x的范围,找出其中的整数,代入直线l1、l2的方程求出y的整数值,即得点Q的坐标.点评:本题考查点轨迹方程的求法,本题考查直线和圆的位置关系,判断符合条件的点均在直线l1、l2上,是解题的关键.

练习册系列答案
相关题目
如图,已知椭圆C的中心在原点O,焦点在 轴上,长轴长是短轴
轴上,长轴长是短轴
长的2倍,且经过点M .
平行于OM的直线
.
平行于OM的直线 在
在 轴上的截距为
轴上的截距为
 并交椭
并交椭
圆C于A、B两个不同点.
(1)求椭圆C的标准方程;
(2)求 的取值范围;
的取值范围;
|
 轴始终围成一个等腰三角形.
轴始终围成一个等腰三角形.

 过点
过点 ,离心率
,离心率 ,若点M(x,y)在椭圆C上,则点
,若点M(x,y)在椭圆C上,则点 称为点M的一个“椭点”,直线l交椭圆C于A、B两点,若点A、B的“椭点”分别是P、Q,且以PQ为直径的圆经过坐标原点O.
称为点M的一个“椭点”,直线l交椭圆C于A、B两点,若点A、B的“椭点”分别是P、Q,且以PQ为直径的圆经过坐标原点O. 过点
过点 ,离心率
,离心率 ,若点M(x,y)在椭圆C上,则点
,若点M(x,y)在椭圆C上,则点 称为点M的一个“椭点”,直线l交椭圆C于A、B两点,若点A、B的“椭点”分别是P、Q,且以PQ为直径的圆经过坐标原点O.
称为点M的一个“椭点”,直线l交椭圆C于A、B两点,若点A、B的“椭点”分别是P、Q,且以PQ为直径的圆经过坐标原点O.