F1.F2是椭圆$\frac{x^2}{25}$+$\frac{y^2}{16}$=1的两焦点.AB是过F2的弦.则△ABF1的周长为20．题目和参考答案——青夏教育精英家教网——

题目内容

14．F₁、F₂是椭圆$\frac{x^2}{25}$+$\frac{y^2}{16}$=1的两焦点，AB是过F₂的弦，则△ABF₁的周长为20．

分析根据椭圆的方程算出a=5，由椭圆的定义得到|AF₁|+|AF₂|=|BF₁|+|BF₂|=2a=10，由此将△ABF₁的周长分成|AF₁|+|AF₂|、|BF₁|+|BF₂|两部分，即可得到所求△ABF₁的周长

解答解：∵椭圆的方程为$\frac{x^2}{25}$+$\frac{y^2}{16}$=1，
∴a=5，
根据椭圆的定义，得|AF₁|+|AF₂|=|BF₁|+|BF₂|=2a=10，
∴△ABF₁的周长|AF₁|+|BF₁|+|AB|=（|AF₁|+|AF₂|）+（|BF₁|+|BF₂|）=20，
故答案为：20．

点评本题给出椭圆经过右焦点的弦AB与左焦点F₁构成的三角形，求△ABF₁的周长．着重考查了椭圆的定义与标准方程的知识，属于基础题．

练习册系列答案

成功训练计划系列答案

倍速训练法直通中考考点系列答案

浙江名卷系列答案

励耘活页系列答案

一卷搞定系列答案

名校作业本系列答案

提分教练系列答案

尖子生学案系列答案

满分训练设计系列答案

轻巧夺冠周测月考直通名校系列答案

相关题目

4．已知椭圆c₁：$\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1的左、右焦点分别为F₁，F₂，过点F₁作垂直于x轴的直线l₁，直线l₂垂直l₁于点P，线段PF₂的垂直平分线交l₂于点M
（1）求点M的轨迹C₂的方程
（2）过点F₂作两条互相垂直的直线AC，BD，且分别交椭圆于A，B，C，D，求四边形ABCD面积的最小值．

5．设0≤x≤2，则函数f（x）=$\frac{1}{2}$×4^x-3•2^x+5的最大值是$\frac{5}{2}$，最小值是$\frac{1}{2}$．

2．设x，y满足约束条件$\left\{\begin{array}{l}x≥0\\ y≥x\\ 4x+3y≤12\end{array}\right.$，则$\frac{2y-x+1}{x+1}$的最大值是9．

9．已知cosαcosβ=cosα+cosβ+3，则sin（α+β）=0．

19．在锐角三角形ABC中，a，b，c是角A，B，C的对边，已知（b²+c²-a²）tanA=$\sqrt{3}$bc
（1）求角A的大小，
（2）若f（B）=sinBcosB-$\sqrt{3}{cos^2}B+\sqrt{3}$，求f（B）范围．

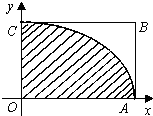如图，曲线AC的方程为$\frac{x^2}{9}+\frac{y^2}{4}$═1（0≤x≤3，0≤y≤2），为估计椭圆$\frac{x^2}{9}+\frac{y^2}{4}$═1的面积，现采用随机模拟方式产生x∈（0，3），y∈（0，2）的200个点（x，y），经统计，落在图中阴影部分的点共157个，则可估计椭圆$\frac{x^2}{9}+\frac{y^2}{4}$═1的面积是18.84．（精确到0.01）

3．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{3}}{2}$，短轴一个端点到右焦点的距离为2，直线l过点P（-1，0）且与曲线C交于A，B两点．
（Ⅰ）求椭圆C的方程；
（Ⅱ）△AOB的面积是否存在最大值，若存在，求出△AOB的面积，若不存在，说明理由．

4．若直线x+2y-3=0，kx+y-1=0，x轴的正半轴和y轴的正半轴所围成的四边形有外接圆，且k＜0，则实数k的值为-2．