题目内容
设命题p:实数x满足x2-4ax+3a2<0,其中a>0,命题q:实数x满足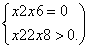
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若非p是非q的充分不必要条件,求实数a的取值范围.
解 (1)由x2-4ax+3a2<0得(x-3a)(x-a)<0.
又a>0,所以a<x<3a,
当a=1时,1<x<3,即p为真命题时,
实数x的取值范围是1<x<3.
由 解得
解得
即2<x≤3.
所以q为真时实数x的取值范围是2<x≤3.
若p∧q为真,则 ⇔2<x<3,
⇔2<x<3,
所以实数x的取值范围是(2,3).
(2) 非p是非q的充分不必要条件,
即非p⇒非q且非qD非p.
设A={x|x≤a,或x≥3a},B={x|x≤2,或x>3},
则A B.
B.
所以0<a≤2且3a>3,即1<a≤2.所以实数a的取值范围是(1,2].

练习册系列答案
相关题目
 平面ABC.
平面ABC.
 ;
; ,
, ,
, ,试求该简单组合体的体积V.
,试求该简单组合体的体积V. ,则f(x)的“姊妹点对”有( )
,则f(x)的“姊妹点对”有( ) ” 的逆否命题是 .
” 的逆否命题是 . 为 ( )
为 ( ) +2 B.Δx+2 C. Δx-
+2 B.Δx+2 C. Δx-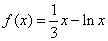 (x>0),则y=f(x) ( )
(x>0),则y=f(x) ( )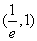 ,(1,e)内均有零点 B. 在区间
,(1,e)内均有零点 B. 在区间
 满足约束条件
满足约束条件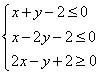 ,若
,若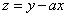 取得最大值的最优解不唯一,则实数
取得最大值的最优解不唯一,则实数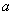 的值为
的值为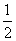 或
或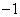 B.2或
B.2或