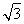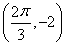题目内容
已知函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ< )的周期为π,且图象上一个最低点为M
)的周期为π,且图象上一个最低点为M .
.
(1)求f(x)的解析式;
(2)当x∈ 时,求f(x)的最值.
时,求f(x)的最值.
(1)f(x)=2sin (2)最小值1,最大值
(2)最小值1,最大值 .
.
【解析】(1)由最低点为M ,得A=2.由T=π,得ω=
,得A=2.由T=π,得ω= =
= =2.
=2.
由点M 在图象上得2sin
在图象上得2sin =-2,
=-2,
即sin =-1,∴
=-1,∴ +φ=2kπ-
+φ=2kπ- (k∈Z),
(k∈Z),
即φ=2kπ- ,k∈Z.又φ∈
,k∈Z.又φ∈ ,∴φ=
,∴φ= ,∴f(x)=2sin
,∴f(x)=2sin .
.
(2)∵x∈ ,∴2x+
,∴2x+ ∈
∈ .
.
∴当2x+ =
= ,即x=0时,f(x)取得最小值1;
,即x=0时,f(x)取得最小值1;
当2x+ =
= ,即x=
,即x= 时,f(x)取得最大值
时,f(x)取得最大值

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目