题目内容
(1)若任意直线l过点F(0,1),且与函数f(x)=
x2的图象C交于两个不同的点A,B,分别过点A,B作C的切线,两切线交于点M,证明:点M的纵坐标是一个定值,并求出这个定值;
(2)若不等式f(x)≥g(x)恒成立,g(x)=alnx(a>o)求实数a的取值范围;
(3)求证:
+
+
+…
<
,(其中e为无理数,约为2.71828).
| 1 |
| 4 |
(2)若不等式f(x)≥g(x)恒成立,g(x)=alnx(a>o)求实数a的取值范围;
(3)求证:
| ln24 |
| 24 |
| ln34 |
| 34 |
| ln44 |
| 44 |
| lnn4 |
| n4 |
| 2 |
| e |
分析:(1)设A(x1,y1),B(x2,y2),分别求出在点A,B处的切线方程,求出两切线的交点M的纵坐标,即可得到结论;
(2)令F(x)=f(x)-g(x),然后利用导数研究F(x)的最小值,使F(x)的最小值大于等于0即可,从而求出a的取值范围;
(3)由(2)可知,取a=
有
≥
lnx 化简得:
≤
,再变形得:
≤
,然后利用叠加法,以及裂项求和法可证得结论.
(2)令F(x)=f(x)-g(x),然后利用导数研究F(x)的最小值,使F(x)的最小值大于等于0即可,从而求出a的取值范围;
(3)由(2)可知,取a=
| e |
| 2 |
| x2 |
| 4 |
| e |
| 2 |
| 2lnx |
| x2 |
| 1 |
| e |
| lnx4 |
| x4 |
| 2 |
| ex2 |
解答:证明:(1)设A(x1,y1),B(x2,y2),由题意知AB的斜率必存在 设AB:y=kx+1代入y=
x2
得 x2-4kx-4=0∴x1x2=-4
∵f(x)=
x2∴f′(x)=
∴kAM=
,kBM=
,
∴AM:y-
=
(x-x1),
化简得:AM:y=
x-
同理:BM:y=
x-
,解得:y=
=-1
(2)令:F(x)=f(x)-g(x)=
x2-alnx(a>0,x>0),
∴F′(x)=
-
=
令 F′(x)=0 得:x=
所以 当x∈(0,
)时F′(x)<0 即F(x)在区间(0,
)上单调递减;
所以 当x∈(
,+∞)时F′(x)>0即即F(x)在区间(
,+∞)上单调递增;
∴y=F(x)在x=
时取得最小值,要f(x)≥g(x)恒成立,只要F(
)≥0
即
-aln
≥0,解得a≤
(3)由(2)可知,取a=
有
≥
lnx 化简得:
≤
变形得:
≤
∴
+
+
+…
<
(
+
+
+…+
)
<
(
+
+…+
)=
(1-
+
-
+…+
-
)=
(1-
)<
| 1 |
| 4 |
得 x2-4kx-4=0∴x1x2=-4
∵f(x)=
| 1 |
| 4 |
| x |
| 2 |
∴kAM=
| x1 |
| 2 |
| x2 |
| 2 |
∴AM:y-
| ||
| 4 |
| x1 |
| 2 |
化简得:AM:y=
| x1 |
| 2 |
| ||
| 4 |
同理:BM:y=
| x2 |
| 2 |
| ||
| 4 |
| x1x2 |
| 4 |
(2)令:F(x)=f(x)-g(x)=
| 1 |
| 4 |
∴F′(x)=
| x |
| 2 |
| a |
| x |
| x2-2a |
| 2x |
令 F′(x)=0 得:x=
| 2a |
所以 当x∈(0,
| 2a |
| 2a |
所以 当x∈(
| 2a |
| 2a |
∴y=F(x)在x=
| 2a |
| 2a |
即
| x |
| 2 |
| 2a |
| e |
| 2 |
(3)由(2)可知,取a=
| e |
| 2 |
| x2 |
| 4 |
| e |
| 2 |
| 2lnx |
| x2 |
| 1 |
| e |
变形得:
| lnx4 |
| x4 |
| 2 |
| ex2 |
∴
| ln24 |
| 24 |
| ln34 |
| 34 |
| ln44 |
| 44 |
| lnn4 |
| n4 |
| 2 |
| e |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 42 |
| 1 |
| n2 |
<
| 2 |
| e |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| (n-1)n |
| 2 |
| e |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-1 |
| 1 |
| n |
| 2 |
| e |
| 1 |
| n |
| 2 |
| e |
点评:本题主要考查了恒成立问题,以及不等式的证明和裂项求和法的应用,同时考查了转化能力,属于难题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
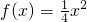 的图象C于两个不同的点A,B过点A,BC,两切线交于点M
的图象C于两个不同的点A,B过点A,BC,两切线交于点M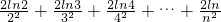
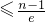 ,(其中e自然对数的底数,n≥2,n∈N).
,(其中e自然对数的底数,n≥2,n∈N).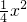 的图象C交于两个不同的点A,B,分别过点A,B作C的切线,两切线交于点M,证明:点M的纵坐标是一个定值,并求出这个定值;
的图象C交于两个不同的点A,B,分别过点A,B作C的切线,两切线交于点M,证明:点M的纵坐标是一个定值,并求出这个定值;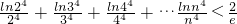 ,(其中e为无理数,约为2.71828).
,(其中e为无理数,约为2.71828). 的图象C交于两个不同的点A,B,分别过点A,B作C的切线,两切线交于点M,证明:点M的纵坐标是一个定值,并求出这个定值;
的图象C交于两个不同的点A,B,分别过点A,B作C的切线,两切线交于点M,证明:点M的纵坐标是一个定值,并求出这个定值; ,(其中e为无理数,约为2.71828).
,(其中e为无理数,约为2.71828).