题目内容
定义在实数集R上的函数f(x),如果存在函数g(x)=Ax+B(A,B为常数)使得f(x)≥g(x)对任意的x∈R都成立,则称g(x)为函数f(x)的一个承托函数,则下列说法正确的是
- A.函数f(x)=x2-2x不存在承托函数
- B.g(x)=x为函数f(x)=sinx的一个承托函数
- C.g(x)=x为函数f(x)=ex-1的一个承托函数
- D.函数
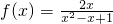 不存在承托函数
不存在承托函数
C
分析:函数g(x)=Ax+B(A,B为常数)是函数f(x)的一个承托函数,即说明函数f(x)的图象恒在函数g(x)的上方(至多有一个交点)A、g(x)=-1是函数f(x)=x2-2x的一个依托函数;故A做;B、举例可以说明,当x= 时,可知f(x)<g(x),可知结论错误;C、要说明g(x)=x为函数f(x)=ex-1的一个承托函数;即证明F(x)=ex-x-1的图象恒在x轴上方;④g(x)=-1是函数
时,可知f(x)<g(x),可知结论错误;C、要说明g(x)=x为函数f(x)=ex-1的一个承托函数;即证明F(x)=ex-x-1的图象恒在x轴上方;④g(x)=-1是函数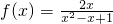 的一个依托函数,因此D错.
的一个依托函数,因此D错.
解答:A、令g(x)=-1,则总有f(x)≥g(x)对任意的x∈R都成立,因此g(x)=-1是函数f(x)=x2-2x的一个依托函数,故A错;
B、令x= ,则g(
,则g( )=
)= >f(
>f( )=1,因此g(x)=x不是函数f(x)=sinx的一个承托函数,故B错;
)=1,因此g(x)=x不是函数f(x)=sinx的一个承托函数,故B错;
C、令F(x)=ex-x-1,F′(x)=ex-1=0,得x=0,
当x<0时,F′(x)<0,F(x)单调递减,
当x>0时,F′(x)>0,F(x)单调递增,
∴当x=0时,F(x)取最小值:0,
即F(x)=ex-x-1≥0恒成立,即f(x)≥g(x)恒成立,故B正确;
D、令g(x)=-1,则 =
=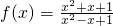 >0,
>0,
∴总有f(x)≥g(x)对任意的x∈R都成立,因此g(x)=-1是函数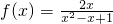 的一个依托函数,故D错;
的一个依托函数,故D错;
故选C.
点评:本题是以抽象函数为依托,考查学生的创新能力,属中档题,抽象函数是相对于给出具体解析式的函数来说的,它虽然没有具体的表达式,但是有一定的对应法则,满足一定的性质,这种对应法则及函数的相应的性质是解决问题的关键.
分析:函数g(x)=Ax+B(A,B为常数)是函数f(x)的一个承托函数,即说明函数f(x)的图象恒在函数g(x)的上方(至多有一个交点)A、g(x)=-1是函数f(x)=x2-2x的一个依托函数;故A做;B、举例可以说明,当x=
 时,可知f(x)<g(x),可知结论错误;C、要说明g(x)=x为函数f(x)=ex-1的一个承托函数;即证明F(x)=ex-x-1的图象恒在x轴上方;④g(x)=-1是函数
时,可知f(x)<g(x),可知结论错误;C、要说明g(x)=x为函数f(x)=ex-1的一个承托函数;即证明F(x)=ex-x-1的图象恒在x轴上方;④g(x)=-1是函数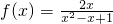 的一个依托函数,因此D错.
的一个依托函数,因此D错.解答:A、令g(x)=-1,则总有f(x)≥g(x)对任意的x∈R都成立,因此g(x)=-1是函数f(x)=x2-2x的一个依托函数,故A错;
B、令x=
 ,则g(
,则g( )=
)= >f(
>f( )=1,因此g(x)=x不是函数f(x)=sinx的一个承托函数,故B错;
)=1,因此g(x)=x不是函数f(x)=sinx的一个承托函数,故B错;C、令F(x)=ex-x-1,F′(x)=ex-1=0,得x=0,
当x<0时,F′(x)<0,F(x)单调递减,
当x>0时,F′(x)>0,F(x)单调递增,
∴当x=0时,F(x)取最小值:0,
即F(x)=ex-x-1≥0恒成立,即f(x)≥g(x)恒成立,故B正确;
D、令g(x)=-1,则
 =
=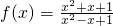 >0,
>0,∴总有f(x)≥g(x)对任意的x∈R都成立,因此g(x)=-1是函数
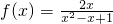 的一个依托函数,故D错;
的一个依托函数,故D错;故选C.
点评:本题是以抽象函数为依托,考查学生的创新能力,属中档题,抽象函数是相对于给出具体解析式的函数来说的,它虽然没有具体的表达式,但是有一定的对应法则,满足一定的性质,这种对应法则及函数的相应的性质是解决问题的关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
已知定义在实数集R上的函数f(x)满足f(1)=1,且f(x)的导数f'(x)在R上恒有f′(x)<
(x∈R),则不等式f(x2)<
+
的解集为( )
| 1 |
| 2 |
| x2 |
| 2 |
| 1 |
| 2 |
| A、(1,+∞) |
| B、(-∞,-1) |
| C、(-1,1) |
| D、(-∞,-1)∪(1,+∞) |
定义在实数集R上的函数f(x),如果存在函数g(x)=Ax+B(A,B为常数)使得f(x)≥g(x)对任意的x∈R都成立,则称g(x)为函数f(x)的一个承托函数,则下列说法正确的是( )
| A、函数f(x)=x2-2x不存在承托函数 | ||
| B、g(x)=x为函数f(x)=sinx的一个承托函数 | ||
| C、g(x)=x为函数f(x)=ex-1的一个承托函数 | ||
D、函数f(x)=
|