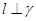题目内容
(本小题满分14分)如图,平面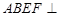 平面
平面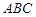 ,四边形
,四边形 为矩形,△
为矩形,△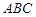 为等边三角形.
为等边三角形.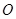 为
为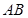 的中点,
的中点,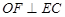 .
.
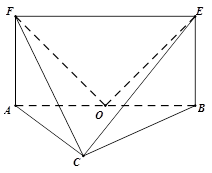
(1)求证: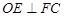 ;
;
(2)求二面角 的正切值.
的正切值.
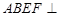 平面
平面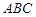 ,四边形
,四边形 为矩形,△
为矩形,△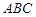 为等边三角形.
为等边三角形.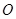 为
为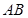 的中点,
的中点,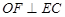 .
.
(1)求证:
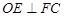 ;
;(2)求二面角
 的正切值.
的正切值.(1)详见解析;(2)

试题分析:(1)连接
 ,要证
,要证 ,只需证明
,只需证明 面
面 ,只需证明
,只需证明 , 由已知面面垂直,易证
, 由已知面面垂直,易证 ,所以
,所以 ,
, 面
面 ,得到
,得到 ,因为
,因为 ,易证
,易证 ,所以
,所以 面
面 ,得
,得 ,得证
,得证 面
面 ,即证
,即证 ;(2)由(1),得
;(2)由(1),得 .不妨设
.不妨设 ,则
,则 .因为
.因为 为等边三角形,则
为等边三角形,则
过
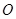 作
作 ,垂足为
,垂足为 ,连接
,连接 ,则
,则 就是二面角
就是二面角 的平面角,易证
的平面角,易证 ,求出.
,求出.试题解析:(1)证明:连结
 ,因
,因 ,
,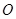 是
是 的中点,
的中点,
故
 . 1分
. 1分又因平面
 平面
平面 ,
,故
 平面
平面 ,
,于是
 . 3分
. 3分又
 ,
,所以
 平面
平面 ,
,所以
 , 5分
, 5分又因
 ,故
,故 平面
平面 ,
,所以
 . 7分
. 7分(2)由(1),得
 .不妨设
.不妨设 ,则
,则 .
.因为
 为等边三角形,则
为等边三角形,则 9分
9分过
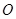 作
作 ,垂足为
,垂足为 ,连接
,连接 ,
,则
 就是二面角
就是二面角 的平面角. 11分
的平面角. 11分在
 中,
中, ,
, ,
, ,
,所以
 ,又
,又 ,所以
,所以
即二面角
 的正切值为
的正切值为 . 14分
. 14分
练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
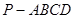 中,底面
中,底面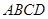 为梯形,
为梯形,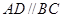 ,
,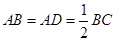 ,
,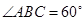 ,平面
,平面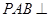 平面
平面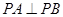 .
.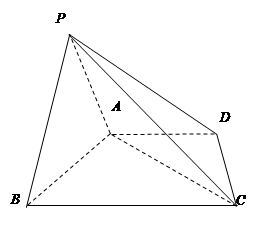
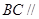 平面
平面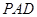 ;
;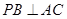 ;
;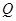 ,到四棱锥
,到四棱锥 中,
中,
 ;
; 与直线BD所成的角
与直线BD所成的角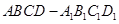 中,E为
中,E为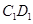 的中点.
的中点.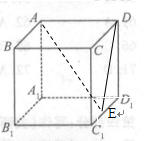
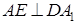 ;
;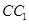 所成的角的正弦值.
所成的角的正弦值.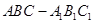 中,四边形
中,四边形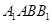 为菱形,
为菱形,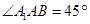 ,四边形
,四边形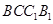 为矩形,若
为矩形,若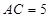 ,
,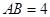 ,
,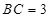 .
.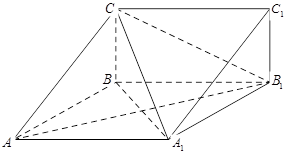
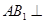 面
面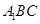 ;
;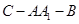 的余弦值;
的余弦值;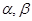 和直线
和直线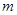 ,给出条件:
,给出条件: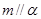 ;②
;②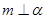 ;③
;③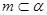 ;④
;④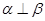 ;⑤
;⑤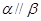 .
.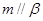 ;(2)当满足条件 时,有
;(2)当满足条件 时,有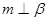 .
. 中,
中,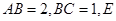 为
为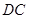 的中点,
的中点,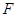 为线段
为线段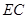 (端点除外)上一动点,现将
(端点除外)上一动点,现将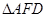 沿
沿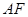 折起,使平面
折起,使平面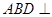 平面
平面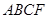 .在平面
.在平面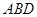 内过点
内过点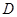 作
作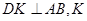 为垂足,设
为垂足,设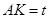 ,则
,则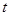 的取值范围是________
的取值范围是________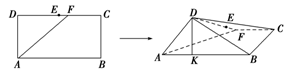
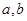 以及平面
以及平面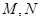 ,下列命题中正确的是 ( )
,下列命题中正确的是 ( )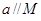 ,
,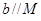 ,则
,则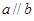
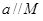 ,
,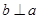 ,则
,则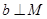
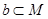 ,且
,且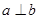 ,则
,则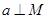
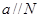 ,则
,则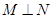
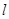 是一条直线,
是一条直线,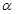 ,
,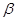 ,
,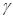 是不同的平面,则下列说法不正确的是( )
是不同的平面,则下列说法不正确的是( )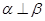 ,那么
,那么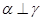 ,
,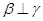 ,
,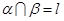 ,那么
,那么