题目内容
定义在R上的函数 既是奇函数又是周期函数,若
既是奇函数又是周期函数,若 的最小正周期是
的最小正周期是 ,且当
,且当 时,
时,  ,则
,则 的值为 ( )
的值为 ( )
A. | B. | C. | D. |
A
解析试题分析:定义在R上的函数f(x)既是偶函数又是周期函数,若f(x)的最小正周期是π,且当 时,
时, ,
,
所以, =f(-
=f(- )=-f(
)=-f( )=-cos
)=-cos =
= .
.
故选A。
考点:函数的周期性,奇偶性,特殊角的三角函数值。
点评:中档题,利用函数的周期性、奇偶性灵活的转化是解题的关键。

练习册系列答案
相关题目
 ,若
,若 ,则
,则 ( )
( )
| A.0 | B.3 | C.-1 | D.-2 |
要得到函数 的图象,只须将
的图象,只须将 的图象上的所有的点( )
的图象上的所有的点( )
A.向左平移 个单位长度 个单位长度 | B.向右平移 个单位长度 个单位长度 |
C.向左平移 个单位长度 个单位长度 | D.向右平移 个单位长度 个单位长度 |
函数 是( )
是( )
A.最小正周期为 的偶函数 的偶函数 | B.最小正周期为 的奇函数 的奇函数 |
C.最小正周期为 的偶函数 的偶函数 | D.最小正周期为 的奇函数 的奇函数 |
若角 的终边上有一点P(a,-2),则实数a的值为( )
的终边上有一点P(a,-2),则实数a的值为( )
A. | B. | C. | D. |
已知角α的终边上一点的坐标为(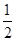 ,-
,- ),则角α的正弦值为( )
),则角α的正弦值为( )
A.- | B. | C.-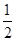 | D.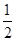 |
A为△ABC的内角,且A为锐角,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
 的定义域为[a,b],值域为[-2,1],则
的定义域为[a,b],值域为[-2,1],则 的值不可能是 ( )
的值不可能是 ( )



 的图象沿轴向左平移
的图象沿轴向左平移 个单位后,得到一个偶函数的图象,则
个单位后,得到一个偶函数的图象,则 的一个可能取值为( )
的一个可能取值为( )


