题目内容
对于函数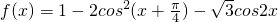 ,给出下列四个命题:
,给出下列四个命题:
(1)函数在区间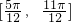 上是减函数;
上是减函数;
(2)直线 是函数图象的一条对称轴;
是函数图象的一条对称轴;
(3)函数f(x)的图象可由函数y=2sin2x的图象向右平移 而得到;
而得到;
(4)若 R,则f(x)=f(2-x),且的值域是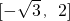 .
.
其中正确命题的个数是
- A.1
- B.2
- C.3
- D.4
A
分析:由三角函数的恒等变换,把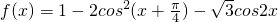 等价转化为f(x)=2sin(2x-
等价转化为f(x)=2sin(2x- ),由此能求出结果.
),由此能求出结果.
解答:∵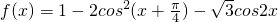
=-cos(2x+ )-
)-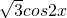
=sin2x-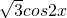
=2sin(2x- ),
),
所以:f(x)的减区间满足: ,k∈Z,
,k∈Z,
解得f(x)的减区间是[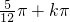 ,
,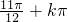 ],k∈Z,
],k∈Z,
故函数在区间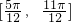 上是减函数,即(1)正确;
上是减函数,即(1)正确;
f(x)的对称轴方程满足:2x- =kπ+
=kπ+ ,k∈Z,
,k∈Z,
即x= ,k∈Z,
,k∈Z,
故直线 不是函数图象的一条对称轴,即(2)不正确;
不是函数图象的一条对称轴,即(2)不正确;
函数y=2sin2x的图象向右平移 得到y=2sin(2x-
得到y=2sin(2x- )≠2sin(2x-
)≠2sin(2x- ),故(3)不正确;
),故(3)不正确;
f(x)≠f(2-x),故(4)不正确.
故选A.
点评:本题考查命题的真假判断的应用,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化和三角函数的合理运用.
分析:由三角函数的恒等变换,把
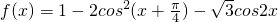 等价转化为f(x)=2sin(2x-
等价转化为f(x)=2sin(2x- ),由此能求出结果.
),由此能求出结果.解答:∵
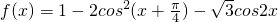
=-cos(2x+
 )-
)-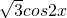
=sin2x-
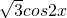
=2sin(2x-
 ),
),所以:f(x)的减区间满足:
 ,k∈Z,
,k∈Z,解得f(x)的减区间是[
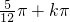 ,
,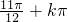 ],k∈Z,
],k∈Z,故函数在区间
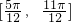 上是减函数,即(1)正确;
上是减函数,即(1)正确;f(x)的对称轴方程满足:2x-
 =kπ+
=kπ+ ,k∈Z,
,k∈Z,即x=
 ,k∈Z,
,k∈Z,故直线
 不是函数图象的一条对称轴,即(2)不正确;
不是函数图象的一条对称轴,即(2)不正确;函数y=2sin2x的图象向右平移
 得到y=2sin(2x-
得到y=2sin(2x- )≠2sin(2x-
)≠2sin(2x- ),故(3)不正确;
),故(3)不正确;f(x)≠f(2-x),故(4)不正确.
故选A.
点评:本题考查命题的真假判断的应用,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化和三角函数的合理运用.

练习册系列答案
相关题目
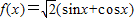 ,给出下列四个命题:
,给出下列四个命题: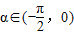 ,使
,使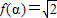 ;
; 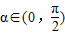 ,使f(x-α)=f(x+α)恒成立;
,使f(x-α)=f(x+α)恒成立;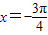 对称;
对称;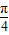 就能得到y=-2cosx的图象
就能得到y=-2cosx的图象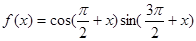 ,给出下列四个结论:①函数
,给出下列四个结论:①函数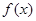 的最小正周期为
的最小正周期为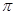 ;②若
;②若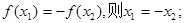 ③
③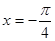 对称;④
对称;④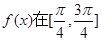 上是减函数,其中正确结论的个数为 ( )
上是减函数,其中正确结论的个数为 ( )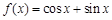 ,给出下列四个命题:
,给出下列四个命题: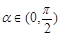 ,使
,使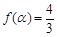 ;
;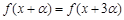 恒成立;
恒成立;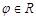 ,使函数
,使函数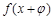 的图象关于y轴对称;
的图象关于y轴对称;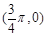 对称.
对称. ,给出下列四个结论:①函数
,给出下列四个结论:①函数 的最小正周期为
的最小正周期为 ;②若
;②若 ③
③ 对称;④
对称;④ 上是减函数,其中正确结论的个数为 ( )
上是减函数,其中正确结论的个数为 ( )