题目内容
数列{an}的前n项和记作Sn,满足Sn=2an+3n-12 (n∈N*).
(1)求出数列{an}的通项公式;
(2)若bn=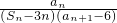 ,求证:b1+b2+…+bn<
,求证:b1+b2+…+bn< ;
;
(3)若cn=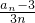 ,且
,且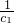 +
+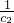 +…+
+…+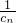 <loga(6-a)对所有的正整数n恒成立,求实数a的取值范围.
<loga(6-a)对所有的正整数n恒成立,求实数a的取值范围.
解:(1)Sn=2an+3n-12,Sn-1=2an-1+3(n-1)-12 (n≥2)
作差化简得到an-2an-1+3=0,所以an-3=2(an-1-3)且a1=9,
所以an-3=6•2n-1,所以an=3•2n+3
(2)bn=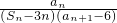 =
= ,∴b1+b2+…+bn=
,∴b1+b2+…+bn= =
=
(3)cn=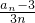 =
= ,令Tn=
,令Tn=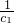 +
+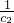 +…+
+…+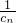
错位相减得 ,∴Tn<2
,∴Tn<2
∵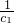 +
+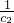 +…+
+…+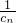 <loga(6-a)对所有的正整数n恒成立,∴loga(6-a)≤2
<loga(6-a)对所有的正整数n恒成立,∴loga(6-a)≤2
当0<a<1时,6-a≤a2,∴a≥2或a≤-3
当1<a<6时,6-a≥a2,∴-3≤a≤2
综上,1≤a≤2.
分析:(1)由Sn=2an+3n-12可得Sn-1=2an-1+3(n-1)-12 (n≥2),两式相减化简可得an-3=2(an-1-3),从而可求数列{an}的通项公式;
(2)bn=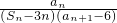 =
= ,从而b1+b2+…+bn=
,从而b1+b2+…+bn= 化简可证
化简可证
(3)cn=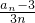 =
= ,令Tn=
,令Tn= 再写一式错位相减可知
再写一式错位相减可知 ,从而Tn<2故问题可转化为loga(6-a)≤2,进而问题得解.
,从而Tn<2故问题可转化为loga(6-a)≤2,进而问题得解.
点评:本题考查构造法求数列的通项、裂项求和,同时考查恒成立问题的处理,解题时要认真审题,仔细解答,注意问题的等价转化.
作差化简得到an-2an-1+3=0,所以an-3=2(an-1-3)且a1=9,
所以an-3=6•2n-1,所以an=3•2n+3
(2)bn=
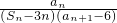 =
= ,∴b1+b2+…+bn=
,∴b1+b2+…+bn= =
=
(3)cn=
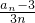 =
= ,令Tn=
,令Tn=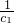 +
+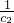 +…+
+…+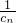
错位相减得
 ,∴Tn<2
,∴Tn<2 ∵
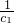 +
+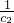 +…+
+…+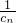 <loga(6-a)对所有的正整数n恒成立,∴loga(6-a)≤2
<loga(6-a)对所有的正整数n恒成立,∴loga(6-a)≤2当0<a<1时,6-a≤a2,∴a≥2或a≤-3
当1<a<6时,6-a≥a2,∴-3≤a≤2
综上,1≤a≤2.
分析:(1)由Sn=2an+3n-12可得Sn-1=2an-1+3(n-1)-12 (n≥2),两式相减化简可得an-3=2(an-1-3),从而可求数列{an}的通项公式;
(2)bn=
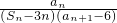 =
= ,从而b1+b2+…+bn=
,从而b1+b2+…+bn= 化简可证
化简可证(3)cn=
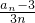 =
= ,令Tn=
,令Tn= 再写一式错位相减可知
再写一式错位相减可知 ,从而Tn<2故问题可转化为loga(6-a)≤2,进而问题得解.
,从而Tn<2故问题可转化为loga(6-a)≤2,进而问题得解.点评:本题考查构造法求数列的通项、裂项求和,同时考查恒成立问题的处理,解题时要认真审题,仔细解答,注意问题的等价转化.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目