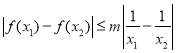题目内容
【题目】函数![]() 且
且![]()
(1)当![]() 时,求函数
时,求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)定义在R上的函数![]() 满足
满足![]() ,当
,当![]() 时,
时,![]() 。若存在
。若存在![]() 满足不等式
满足不等式![]() 且
且![]() 是函数
是函数![]() 的一个零点,求实数a的取值范围。
的一个零点,求实数a的取值范围。
【答案】(1)![]() (2)
(2)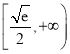
【解析】
(1)将![]() 代入
代入![]() ,求其导函数,得
,求其导函数,得![]() 的值,进而可得切线方程。
的值,进而可得切线方程。
(2)构造函数![]() ,根据已知得到其是奇函数,求导可得
,根据已知得到其是奇函数,求导可得![]() 在
在![]() 上的单调性,将
上的单调性,将![]() 转化为关于
转化为关于![]() 的不等式,利用
的不等式,利用![]() 的单调性解该不等式,可求得
的单调性解该不等式,可求得![]() 的范围,即
的范围,即![]() 的零点的范围,转化为
的零点的范围,转化为![]() 在
在![]() 的范围上有零点,利用导数知识和零点存在性定理,可求出a的取值范围。
的范围上有零点,利用导数知识和零点存在性定理,可求出a的取值范围。
解:(1)当![]() 时,因为
时,因为![]()
所以![]() ,
,
所以![]() ,
,
又![]() ,所以函数
,所以函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,
,
即![]()
(2)令![]() ,因为
,因为![]() ,
,
所以![]() ,
,
所以![]() 为奇函数。
为奇函数。
当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() 在R上单调递减,
在R上单调递减,
又![]() 满足不等式
满足不等式![]() ,即
,即![]() ,
,
所以![]() ,
,
化简得![]() ,所以
,所以![]() ,即
,即![]()
令![]()
因为![]() 是函数
是函数![]() 的一个零点,
的一个零点,
所以![]() 在
在![]() 时有一个零点:
时有一个零点:
当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递减,
上单调递减,
又![]() ,又因为
,又因为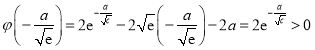 ,
,
所以要使![]() 在
在![]() 时有一个零点,只需
时有一个零点,只需![]() ,解得
,解得![]() ,
,
所以实数a的取值范围为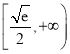

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案【题目】某地区实施“光盘行动”以后,某自助啤酒吧也制定了自己的行动计划,进店的每一位客人需预交![]() 元,啤酒根据需要自己用量杯量取,结账时,根据每桌剩余酒量,按一定倍率收费(如下表),每桌剩余酒量不足
元,啤酒根据需要自己用量杯量取,结账时,根据每桌剩余酒量,按一定倍率收费(如下表),每桌剩余酒量不足![]() 升的,按
升的,按![]() 升计算(如剩余
升计算(如剩余![]() 升,记为剩余
升,记为剩余![]() 升).例如:结账时,某桌剩余酒量恰好为
升).例如:结账时,某桌剩余酒量恰好为![]() 升,则该桌的每位客人还应付
升,则该桌的每位客人还应付![]() 元.统计表明饮酒量与人数有很强的线性相关关系,下面是随机采集的
元.统计表明饮酒量与人数有很强的线性相关关系,下面是随机采集的![]() 组数据
组数据![]() (其中
(其中![]() 表示饮酒人数,
表示饮酒人数,![]() (升)表示饮酒量):
(升)表示饮酒量):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
剩余酒量(单位:升) |
|
|
|
|
|
结账时的倍率 |
|
|
|
|
|
(1)求由这![]() 组数据得到的
组数据得到的![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)小王约了![]() 位朋友坐在一桌饮酒,小王及朋友用量杯共量取了
位朋友坐在一桌饮酒,小王及朋友用量杯共量取了![]() 升啤酒,这时,酒吧服务生对小王说,根据他的经验,小王和朋友量取的啤酒可能喝不完,可以考虑再邀请
升啤酒,这时,酒吧服务生对小王说,根据他的经验,小王和朋友量取的啤酒可能喝不完,可以考虑再邀请![]() 位或
位或![]() 位朋友一起来饮酒,会更划算.试向小王是否该接受服务生的建议?
位朋友一起来饮酒,会更划算.试向小王是否该接受服务生的建议?
参考数据:回归直线的方程是![]() ,其中
,其中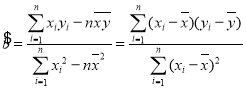 ,
,![]() .
.
【题目】某冰糖橙,甜橙的一种,云南著名特产,以味甜皮薄著称。该橙按照等级可分为四类:珍品、特级、优级和一级(每箱有5kg),某采购商打算订购一批橙子销往省外,并从采购的这批橙子中随机抽取100箱,利用橙子的等级分类标准得到的数据如下表:
等级 | 珍品 | 特级 | 优级 | 一级 |
箱数 | 40 | 30 | 10 | 20 |
(1)若将频率改为概率,从这100箱橙子中有放回地随机抽取4箱,求恰好抽到2箱是一级品的概率:
(2)利用样本估计总体,庄园老板提出两种购销方案供采购商参考:
方案一:不分等级卖出,价格为27元/kg;
方案二:分等级卖出,分等级的橙子价格如下:
等级 | 珍品 | 特级 | 优级 | 一级 |
售价(元/kg) | 36 | 30 | 24 | 18 |
从采购商的角度考虑,应该采用哪种方案?
(3)用分层抽样的方法从这100箱橙子中抽取10箱,再从抽取的10箱中随机抽取3箱,X表示抽取的是珍品等级,求x的分布列及数学期望E(X).
【题目】某高铁站停车场针对小型机动车收费标准如下:2小时内(含2小时)每辆每次收费5元;超过2小时不超过5小时,每增加一小时收费增加3元,不足一小时的按一小时计费;超过5小时至24小时内(含24小时)收费15元封顶。超过24小时,按前述标准重新计费.为了调查该停车场一天的收费情况,现统计1000辆车的停留时间(假设每辆车一天内在该停车场仅停车一次),得到下面的频数分布表:
T(小时) |
|
|
|
|
|
频数(车次) | 600 | 120 | 80 | 100 | 100 |
以车辆在停车场停留时间位于各区间的频率代替车辆在停车场停留时间位于各区间的概率。
(1)X表示某辆车在该停车场停车一次所交费用,求X的概率分布列及期望![]() ;
;
(2)现随机抽取该停车场内停放的3辆车,![]() 表示3辆车中停车费用少于
表示3辆车中停车费用少于![]() 的车辆数,求
的车辆数,求![]() 的概率.
的概率.