题目内容
在△ABC中,角A,B,C的对边分别为a,b,c,且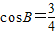 .
.(Ⅰ)求
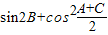 的值;
的值;(Ⅱ)若
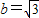 ,求△ABC面积的最大值.
,求△ABC面积的最大值.
【答案】分析:(Ⅰ)通过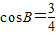 求出
求出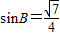 ,利用二倍角以及三角形的内角和化简
,利用二倍角以及三角形的内角和化简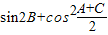 ,即可求出它的值;
,即可求出它的值;
(Ⅱ)利用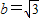 ,结合余弦定理,求出a,c的关系,通过基本不等式求出a,c,然后求出三角形的面积最大值.
,结合余弦定理,求出a,c的关系,通过基本不等式求出a,c,然后求出三角形的面积最大值.
解答:(本小题满分13分)
解:(I)因为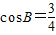 ,所以
,所以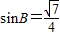 .…(1分)
.…(1分)
又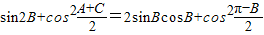 =
=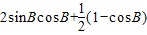
=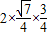 +
+ =
=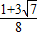 .…(6分)
.…(6分)
(II)由已知得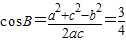 ,…(7分)
,…(7分)
又因为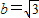 ,所以
,所以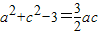 .…(8分)
.…(8分)
又因为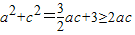 ,
,
所以ac≤6,当且仅当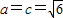 时,ac取得最大值.…(11分)
时,ac取得最大值.…(11分)
此时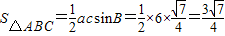 .
.
所以△ABC的面积的最大值为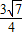 .…(13分)
.…(13分)
点评:本题考查二倍角公式,余弦定理,基本不等式的应用,考查计算能力.
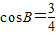 求出
求出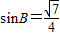 ,利用二倍角以及三角形的内角和化简
,利用二倍角以及三角形的内角和化简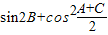 ,即可求出它的值;
,即可求出它的值;(Ⅱ)利用
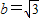 ,结合余弦定理,求出a,c的关系,通过基本不等式求出a,c,然后求出三角形的面积最大值.
,结合余弦定理,求出a,c的关系,通过基本不等式求出a,c,然后求出三角形的面积最大值.解答:(本小题满分13分)
解:(I)因为
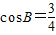 ,所以
,所以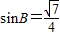 .…(1分)
.…(1分)又
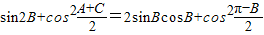 =
=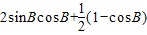
=
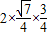 +
+ =
=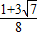 .…(6分)
.…(6分)(II)由已知得
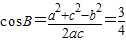 ,…(7分)
,…(7分)又因为
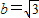 ,所以
,所以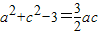 .…(8分)
.…(8分)又因为
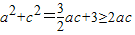 ,
,所以ac≤6,当且仅当
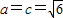 时,ac取得最大值.…(11分)
时,ac取得最大值.…(11分)此时
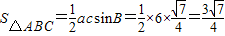 .
.所以△ABC的面积的最大值为
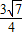 .…(13分)
.…(13分)点评:本题考查二倍角公式,余弦定理,基本不等式的应用,考查计算能力.

练习册系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |