题目内容
已知点F（0，1），点P在x轴上运动，M点在y轴上，N为动点，且满足| PM |
| PF |
| PN |
| PM |
（1）求动点N的轨迹C方程；
（2）由直线y=-1上一点Q向曲线C引两条切线，切点分别为A，B，求证：AQ⊥BQ．
分析：（1）首先根据
+
=0分别表示出P，M的坐标；然后根据
•
=0两个条件即可求出动点N的轨迹C方程．
（2）根据两条直线斜率k均存在，故直接设出两切线方程，代入曲线C的方程，化简为一元二次方程，根据判别式△=0得到一个关系式，根据韦达定理易得出两根之积为-1，即两斜率之积为-1，易得出两直线垂直
| PN |
| PM |
| PM |
| PF |
（2）根据两条直线斜率k均存在，故直接设出两切线方程，代入曲线C的方程，化简为一元二次方程，根据判别式△=0得到一个关系式，根据韦达定理易得出两根之积为-1，即两斜率之积为-1，易得出两直线垂直
解答：解：（1）设N（x，y）．
因
+
=0，
故P的坐标为（
，0），M（0，-y），
于是，
=(-
，-y)，
=(-
，1)．
因
•
=0，
即得曲线C的方程为x2=4y
（2）设Q（m，-1）．
由题意，两条切线的斜率k均存在，
故可设两切线方程为y=k（x-m）-1．
将上述方程代入x2=4y，
得x2-4kx+4km+4=0．
依题意，△=（-4k）2-4（4km+4）=0，
即k2-mk-1=0．
上述方程的两根即为两切线的斜率，
由根与系数的关系，其积为-1，即它们所在直线互相垂直
∴AQ⊥BQ
因
| PN |
| PM |
故P的坐标为（
| x |
| 2 |
于是，
| PM |
| x |
| 2 |
| PF |
| x |
| 2 |
因
| PM |
| PF |
即得曲线C的方程为x2=4y
（2）设Q（m，-1）．
由题意，两条切线的斜率k均存在，
故可设两切线方程为y=k（x-m）-1．
将上述方程代入x2=4y，
得x2-4kx+4km+4=0．
依题意，△=（-4k）2-4（4km+4）=0，
即k2-mk-1=0．
上述方程的两根即为两切线的斜率，
由根与系数的关系，其积为-1，即它们所在直线互相垂直
∴AQ⊥BQ
点评：本题考查求点的运动轨迹方程问题和直线与圆锥曲线相切问题，涉及到一元二次方程判别式与韦达定理的问题，属于难题
练习册系列答案
口算题天天练系列答案
相关题目
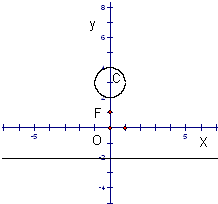如图，已知点F（0，1），直线L：y=-2，及圆C：x2+（y-3）2=1．
（2013•嘉定区二模）如图，已知点F（0，1），直线m：y=-1，P为平面上的动点，过点P作m的垂线，垂足为点Q，且