题目内容
如图,在棱长为4的正方体ABCD—A1B1C1D1中,O是正方形A1B1C1D1的中心,点P在棱CC1上,且CC1=4CP.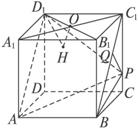
(1)求直线AP与平面BCC1B1所成的角的大小(结果用反三角函数值表示);
(2)设O点在平面D1AP上的射影是H,求证:D1H⊥AP;
(3)求点P到平面ABD1的距离.
解:如图,(1)连结BP.

∵AB⊥平面BCC1B1,
∴AP与平面BCC1B1所成的角就是∠APB.
∵CC1=4CP,CC1=4,
∴CP=1.
在Rt△PBC中,∠PCB为直角,BC=4,CP=1,故BP=![]() .
.
在Rt△APB中,∠ABP为直角,tan∠APB=![]() ,
,
∴∠APB=arctan![]() ,
,
即直线AP与平面BCC1B1所成的角为arctan![]() .
.
(2)连结A1C1,B1D1.
∵四边形A1B1C1D1是正主形,∴D1O⊥A1C1.
又AA1⊥底面A1B1C1D1,∴AA1⊥D1O.
∵AA1∩A1C1=A1,∴D1O⊥平面A1APC1.
∵AP![]() 平面A1APC1,∴D1O⊥AP.
平面A1APC1,∴D1O⊥AP.
∵平面D1AP的斜线D1O在这个平面内的射影是D1H.∴D1H⊥AP.
(3)连结BC1,在平面BCC1B1中,过点P作PQ⊥BC1于点Q.
∵AB⊥平面BCC1B1,PQ![]() 平面BCC1B1,
平面BCC1B1,
∴PQ⊥AB.
∴PQ⊥平面ABC1D1.
∴PQ就是点P到平面ABD1的距离.
在Rt△C1PQ中,∠C1QP=90°,∠PC1Q=45°,PC1=3,
∴PQ=![]() ,即点P到平面ABD1的距离为
,即点P到平面ABD1的距离为![]() .
.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
 (2012•温州一模)如图,直线l⊥平面α,垂足为O,正四面体ABCD的棱长为4,C在平面α内,B是直线l上的动点,则当O到AD的距离为最大时,正四面体在平面α上的射影面积为( )
(2012•温州一模)如图,直线l⊥平面α,垂足为O,正四面体ABCD的棱长为4,C在平面α内,B是直线l上的动点,则当O到AD的距离为最大时,正四面体在平面α上的射影面积为( )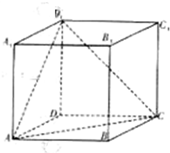 如图,正方体ABCD-A1B1C1D1的棱长为4,点P从B点出发,在正方形BCC1B1的边上按逆针方向按如下规律运动:设第n次运动的路程为an,且
如图,正方体ABCD-A1B1C1D1的棱长为4,点P从B点出发,在正方形BCC1B1的边上按逆针方向按如下规律运动:设第n次运动的路程为an,且 如图,在正三棱柱ABC-A1B1C1中,点D,D1分别为棱BC,B1C1的中点.
如图,在正三棱柱ABC-A1B1C1中,点D,D1分别为棱BC,B1C1的中点.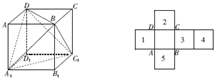 (2011•安徽模拟)下面关于棱长为1的正方体ABCD-A1B1C1D1叙述正确的是
(2011•安徽模拟)下面关于棱长为1的正方体ABCD-A1B1C1D1叙述正确的是 平面
平面 ,垂足为
,垂足为 ,正四面体
,正四面体 的棱长为4,
的棱长为4, 在平面
在平面 是直线
是直线 上的动点,则当
上的动点,则当 的距离为最大时,正四面体在平面
的距离为最大时,正四面体在平面 B.
B. C.
C. D.
D.
