题目内容
5．设某一随机变量X～N（0，1），记P1=P（-2≤X≤-1），P2=P（0≤X≤1），则P1P2的关系是（ ）| A． | P1＜P2 | B． | P1＞P2 | C． | P1=P2 | D． | 无法确定 |
分析 根据变量符合正态分布，和所给的μ和σ的值，根据3σ原则，结合对称性得到结果．
解答 解：∵随机变量X服从正态分布X～N（0，1），
∴P1=P（-2≤X≤-1）=$\frac{1}{2}$×（0.9544-0.6826）=0.1359，P2=P（0≤X≤1）=$\frac{1}{2}$×0.6826=0.3413，
∴P1＜P2，
故选：A．
点评 本题考查正态分布曲线的特点及曲线所表示的意义，考查正态分布中两个量μ和σ的应用，考查曲线的对称性，属于基础题．
练习册系列答案
相关题目
15．执行程序框图，若输入a，b，i的值分别为6，8，0，则输出a和i的值分别为（ ）
| A． | 2，4 | B． | 0，4 | C． | 2，3 | D． | 0，3 |
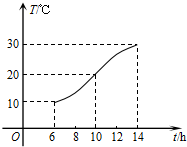某地一天中6时至14时的温度变化曲线近似满足函数T=Asin（ωt+φ）+b（其中$\frac{π}{2}$＜φ＜π），6时至14时期间的温度变化曲线如图所示，它是上述函数的半个周期的图象，那么这一天6时至14时温差的最大值是20°C；图中曲线对应的函数解析式是y=10sin（$\frac{π}{8}$x+$\frac{3π}{4}$）+20，x∈[6，14]．